题目内容
如图，等边三角形ABC的边长为3，D、E分别是AB、AC上的点，且AD=AE=2，将△ADE沿直线DE折叠，点A的落点记为A′，则四边形ADA′E的面积S1与△ABC的面积S2之间的关系是（ ）
A．
B．
C．
D．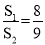
D
【解析】
先根据已知可得到△ADE∽△ABC，从而可得到其相似比与面积比，再根据翻折变换（折叠问题）的性质，从而不难求得四边形ADA′E的面积S1与△ABC的面积S2的面积的比．
解：∵
∠A=∠A，
∴△ADE∽△ABC，相似比是2：3，面积的比是4：9
∵△ADE沿直线DE折叠，点A的落点记为A′，
∴四边形ADA′E的面积S1=2×△ADE的面积，
设△ADE的面积是4a，则△ABC的面积是9a，四边形ADA′E的面积是8a，
∴四边形ADA′E的面积S1与△ABC的面积S2之间的关系是
．
故选D．
练习册系列答案
阅读快车系列答案
相关题目
B．﹣1
C．﹣2
C．
D．
