题目内容
4.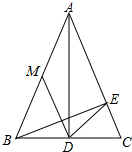 已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AB的中点,联结DE、DM.
已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AB的中点,联结DE、DM.(1)当∠C=70°时(如图),求∠EDM的度数;
(2)当△ABC是钝角三角形时,请画出相应的图形;设∠C=α,用α表示∠EDM(可直接写出).
分析 (1)根据等腰三角形的性质可得∠ABC=70°,D为BC的中点,进而利用直角三角形斜边上的中线的性质得到DE=DC,并利用等腰三角形的性质与三角形内角和定理求出∠EDC的度数,然后利用直角三角形斜边上的中线的性质和等腰三角形的性质可求出∠MDB的度数,再利用平角的定义可求出∠EDM的度数;
(2)首先根据题意画出图形,利用直角三角形斜边上的中线的性质可以得到ED=DC,MD=BM,然后利用等腰三角形的性质可得∠DEC=∠C=α,∠MBD=∠MDB=α,进而利用三角形内角和定理可得∠EDC=180°-2α,再利用平角的定义求解即可.
解答 解:(1)∵AB=AC,AD⊥BC,垂足为D,
∴D为BC中点,∠ABC=∠C=70°,
∵BE⊥AC,∴DE=$\frac{1}{2}$BC=DC,
∴∠DEC=∠C=70°,
∴∠EDC=180°-2×70°=40°,
∵AD⊥BC,M为AC的中点,
∴DM=$\frac{1}{2}$AB=BM,
∴∠MDB=∠ABC=70°,
∴∠EDM=180°-∠EDC-∠BDM=70°;
(2)如图,∵AB=AC,AD⊥BC,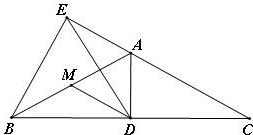
∴D是BC的中点,
又∵BE⊥AC,
∴DE=$\frac{1}{2}$BC=DC,
∴∠DEC=∠C=α,
∴∠EDC=180°-∠DEC-∠C=180°-2α,
∵AB=AC,
∴∠ABC=∠C=α,
又∵M是AB的中点,AD⊥BC,
∴DM=$\frac{1}{2}$AB=BM,
∴∠MBD=∠MDB=α,
∴∠EDM=180°-∠MDB-∠EDC=α.
点评 本题考查了等腰三角形的性质,直角三角形斜边上的中线的性质,三角形内角和定理等知识,熟练掌握并能灵活运用相关的各个定理与性质是解答本题的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
12.若5x=2,5y=$\frac{1}{2}$,则x,y之间的关系为( )
| A. | x,y互为相反数 | B. | x,y互为倒数 | C. | x=y | D. | 无法判断 |
19.不等式2(x-2)≤x-2的正整数解的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.下列命题是真命题的是( )
| A. | 等腰三角形顶角的外角平分线与底边平行 | |
| B. | 等腰三角形的高、中线、角平分线互相重合 | |
| C. | 底角相等的两个等腰三角形全等 | |
| D. | 等腰三角形的一边不可能是另一边的两倍 |
14.已知四边形ABCD是平行四边形,下列结论不正确的是( )
| A. | 当AC=BD时,它是菱形 | B. | 当AC⊥BD时,它是菱形 | ||
| C. | 当∠ABC=90°时,它是矩形 | D. | 当AB=BC时,它是菱形 |


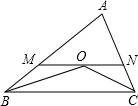 已知:在△ABC中,AB=8cm,AC=6cm,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N,那么△AMN的周长=14cm.
已知:在△ABC中,AB=8cm,AC=6cm,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N,那么△AMN的周长=14cm.