题目内容
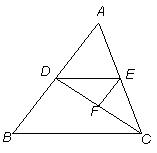
如图，已知∠BDC＋∠EFC＝180°，∠DEF＝∠B．
(1) 求证：∠AED＝∠ACB；
(2) 若D、E、F分别是AB、AC、CD边上的中点，S四边形ADFE＝6，求S△ABC．
 |
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
新课标阶梯阅读训练系列答案口算心算速算应用题系列答案题目内容
如图，已知∠BDC＋∠EFC＝180°，∠DEF＝∠B．
(1) 求证：∠AED＝∠ACB；
(2) 若D、E、F分别是AB、AC、CD边上的中点，S四边形ADFE＝6，求S△ABC．
|
新课标阶梯阅读训练系列答案口算心算速算应用题系列答案
ECA．
； 
中正确的有( )
AB，垂足为F．求证：PD+PE=CF．小军的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF． 小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．
和小俊的思路中任选一种方法，证明PD+PE=CF。