题目内容
如图,⊙C的内接⊿AOB中,AB=AO=4,tan∠AOB=![]() ,抛物线y=ax2+bx经过点A(4,0)与点(-2,6)
,抛物线y=ax2+bx经过点A(4,0)与点(-2,6)
(1)求抛物线的函数解析式.
(2)直线m与⊙C相切于点A交y轴于点D,动点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动,点P的速度为每秒1个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值
 (3)点R在抛物线位于x轴下方部分的图象上,当⊿ROB面积最大时,求点R的坐标.
(3)点R在抛物线位于x轴下方部分的图象上,当⊿ROB面积最大时,求点R的坐标.
解:(1)把点A(4,0)与点(-2,6)代入抛物线y=ax2+bx,得:
![]()
![]() 16a+4b=0 a=
16a+4b=0 a=![]()
4a-2b=6 解得: b= -2
∴抛物线的函数解析式为:y=![]() x2-2x
x2-2x
(2)连AC交OB于E
∵直线m切⊙C于A ∴AC⊥m,∵ 弦 AB=AO ∴ ![]() =
=![]()
∴AC⊥OB ∴m∥OB ∴∠ OAD=∠AOB
∵OA=4 tan∠AOB=![]()
∴OD=OA·tan∠OAD=4×![]() =3
=3
作OF⊥AD于F
OF=OA·sin∠OAD=4×![]() =2.4www. xk b1 .com
=2.4www. xk b1 .com
t秒时,OP=t,DQ=2t,若PQ⊥AD 则FQ=OP= t
DF=DQ-FQ= t ⊿ODF中,t=DF=![]() =1.8秒
=1.8秒
(3)令R(x, ![]() x2-2x) (0<x<4)
x2-2x) (0<x<4)
 作RG⊥y轴于G 作RH⊥OB于H交y轴于I
作RG⊥y轴于G 作RH⊥OB于H交y轴于I
则RG= x OG= ![]() x2+2x
x2+2x
Rt⊿RIG中,∵∠GIR=∠AOB ∴tan∠GIR=![]()
∴IG=![]() x IR=
x IR=![]() x, Rt⊿OIH中,新 课标 第 一网
x, Rt⊿OIH中,新 课标 第 一网
OI=IG-OG=![]() x-(
x-(![]() x2+2x)=
x2+2x)=![]() x2-
x2-![]() x
x
HI=![]() (
(![]() x2-
x2-![]() x)
x)
于是RH=IR-IH=![]() x-
x-![]() (
(![]() x2-
x2-![]() x)
x)
=-![]() x2+
x2+![]() x=-
x=-![]() x2+
x2+![]() x=-
x=-![]() ( x-
( x-![]() )2+
)2+![]()
当x=![]() 时,RH最大。S⊿ROB最大。这时
时,RH最大。S⊿ROB最大。这时![]() x2-2x=
x2-2x=![]() ×(
×(![]() )2-2×
)2-2×![]() =-
=-![]()
∴点R(![]() ,-
,-![]() )
)

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案 如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④
如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④ |
| AD |
 |
| BD |
| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
 如图,⊙O的内接多边形周长为3,⊙O的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( )
如图,⊙O的内接多边形周长为3,⊙O的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( )A、
| ||
B、
| ||
C、
| ||
D、
|
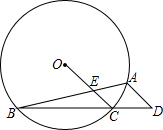 OC交AB于E.
OC交AB于E. 如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=
如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB= 如图,⊙O的内接四边形ABCD中,AB=AD,∠BAD=30°,AC=4,求四边形ABCD的面积.
如图,⊙O的内接四边形ABCD中,AB=AD,∠BAD=30°,AC=4,求四边形ABCD的面积.