题目内容
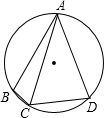
 如图,⊙O的内接四边形ABCD中,AB=AD,∠BAD=30°,AC=4,求四边形ABCD的面积.
如图,⊙O的内接四边形ABCD中,AB=AD,∠BAD=30°,AC=4,求四边形ABCD的面积.分析:根据直径所对的圆周角是直角可得∠ABC=∠D=90°,然后利用“HL”证明Rt△ABC和Rt△ADC全等,根据全等三角形对应角相等求出∠BAC=∠DAC=15°,连接OB,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BOC=30°,过点B作BE⊥AC于E,根据直角三角形30°角所对的直角边等于斜边的一半求出BE,然后求出△ABC的面积,再根据四边形ABCD的面积=S△ABC+S△ACD计算即可得解.
解答: 解:由图可知,AC是⊙O的直径,
解:由图可知,AC是⊙O的直径,
∴∠ABC=∠D=90°,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAC=∠DAC=
∠BAD=
×30°=15°,
连接OB,则OA=OB,
∴∠ABO=∠BAC=15°,
∴∠BOC=∠ABO+∠BAC=15°+15°=30°,
∵AC=4,
∴OB=OA=
AC=
×4=2,
过点B作BE⊥AC于E,
则BE=
OB=
×2=1,
∴S△ABC=
AC•BE=
×4×1=2,
∵Rt△ABC≌Rt△ADC,
∴S△ADC=S△ABC=2,
四边形ABCD的面积=S△ABC+S△ACD=2+2=4.
 解:由图可知,AC是⊙O的直径,
解:由图可知,AC是⊙O的直径,∴∠ABC=∠D=90°,
在Rt△ABC和Rt△ADC中,
|
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAC=∠DAC=
| 1 |
| 2 |
| 1 |
| 2 |
连接OB,则OA=OB,
∴∠ABO=∠BAC=15°,
∴∠BOC=∠ABO+∠BAC=15°+15°=30°,
∵AC=4,
∴OB=OA=
| 1 |
| 2 |
| 1 |
| 2 |
过点B作BE⊥AC于E,
则BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∵Rt△ABC≌Rt△ADC,
∴S△ADC=S△ABC=2,
四边形ABCD的面积=S△ABC+S△ACD=2+2=4.
点评:本题是圆的综合题型,主要考查了直径所对的圆周角是直角,全等三角形的判定与性质,等边对等角的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,作辅助线求出AC边上的高线是解题的关键,也是本题的难点.

练习册系列答案
相关题目
 如图:在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边ABCD的面积为( )
如图:在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边ABCD的面积为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
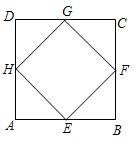
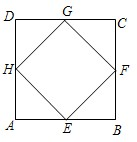 四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.
四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4. 如图:在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边ABCD的面积为
如图:在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边ABCD的面积为


 四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.
四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.