题目内容
已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D,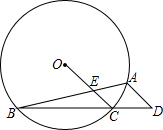 OC交AB于E.
OC交AB于E.(1)求∠D的度数;
(2)求证:AC2=AD•CE;
(3)求
| BC | CD |
分析:(1)根据圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.等边对等角及平行线的性质可求∠D的度数;
(2)乘积的形式通常可以转化为比例的形式,通过证明三角形相似得出.
(3)延长BO交DA的延长线于F,连接OA.通过证明△BOC∽△BFD得出
的值.
(2)乘积的形式通常可以转化为比例的形式,通过证明三角形相似得出.
(3)延长BO交DA的延长线于F,连接OA.通过证明△BOC∽△BFD得出
| BC |
| CD |
解答: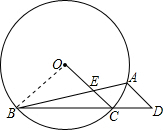 (1)解:如图,连接OB(1分)
(1)解:如图,连接OB(1分)
∵⊙O的内接△ABC中,∠BAC=45°,
∴∠BOC=2∠BAC=90°
∵OB=OC,
∴∠OBC=∠OCB=45°
∵AD∥OC,
∴∠D=∠OCB=45°(2分)
(2)证明:∵∠BAC=45°,∠D=45°,
∴∠BAC=∠D(3分)
∵AD∥OC,
∴∠ACE=∠DAC(4分)
∴△ACE∽△DAC
∴
=
∴AC2=AD•CE(5分)
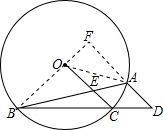
(3)解:方法一:如图,延长BO交DA的延长线于F,连接OA
∵AD∥OC,
∴∠F=∠BOC=90°
∵∠ABC=15°,
∴∠OBA=∠OBC-∠ABC=30°
∵OA=OB,
∴∠FOA=∠OBA+∠OAB=60°,∠OAF=30°、
∴OF=
OA
∵AD∥OC,
∴△BOC∽△BFD
∴
=
∴
=
=
=2,即
的值为2(7分)
方法二:作OM⊥BA于M,设⊙O的半径为r,可得BM=
r,OM=
,∠MOE=30°,
ME=OM•tan30°=
r,BE=
r,AE=
r,所以
=
=2
 (1)解:如图,连接OB(1分)
(1)解:如图,连接OB(1分)∵⊙O的内接△ABC中,∠BAC=45°,
∴∠BOC=2∠BAC=90°
∵OB=OC,
∴∠OBC=∠OCB=45°
∵AD∥OC,
∴∠D=∠OCB=45°(2分)
(2)证明:∵∠BAC=45°,∠D=45°,
∴∠BAC=∠D(3分)
∵AD∥OC,
∴∠ACE=∠DAC(4分)
∴△ACE∽△DAC
∴
| AC |
| DA |
| CE |
| AC |
∴AC2=AD•CE(5分)

(3)解:方法一:如图,延长BO交DA的延长线于F,连接OA
∵AD∥OC,
∴∠F=∠BOC=90°
∵∠ABC=15°,
∴∠OBA=∠OBC-∠ABC=30°
∵OA=OB,
∴∠FOA=∠OBA+∠OAB=60°,∠OAF=30°、
∴OF=
| 1 |
| 2 |
∵AD∥OC,
∴△BOC∽△BFD
∴
| BC |
| BD |
| BO |
| BF |
∴
| BC |
| CD |
| BO |
| OF |
| OA |
| OF |
| BC |
| CD |
方法二:作OM⊥BA于M,设⊙O的半径为r,可得BM=
| ||
| 2 |
| r |
| 2 |
ME=OM•tan30°=
| ||
| 6 |
2
| ||
| 3 |
| ||
| 3 |
| BC |
| CD |
| BE |
| EA |
点评:本题主要考查了相似三角形的判定和性质,同时考查了圆周角定理和平行线的性质,综合性较强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
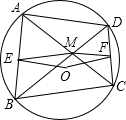 已知:如图,⊙O的内接四边形ABCD的对角线交于点M,点E、F分别为AB、CD的中点.
已知:如图,⊙O的内接四边形ABCD的对角线交于点M,点E、F分别为AB、CD的中点.

 ;
; 的值。
的值。
 的值.
的值.