题目内容
已知x+y+z=0,且x>y>z,则
的取值范围是 .
| y |
| z |
考点:不等式的性质
专题:
分析:先求出y=-x-z,得出
=
=-1-
,再利用x>0,z<0,求解.
| y |
| z |
| -x-z |
| z |
| x |
| z |
解答:解:∵x+y+z=0,
∴y=-x-z,
∴
=
=-1-
,
∵x>y>z,x+y+z=0,
∴x>0,z<0,
∵x=-(y+z)<-2z,
∴-
<2,
∵z=-(x+y)<-2z,
∴-
>
,
∴-
<-1-
<1,即-
<
<1,
故答案为:-
<
<1.
∴y=-x-z,
∴
| y |
| z |
| -x-z |
| z |
| x |
| z |
∵x>y>z,x+y+z=0,
∴x>0,z<0,
∵x=-(y+z)<-2z,
∴-
| x |
| z |
∵z=-(x+y)<-2z,
∴-
| x |
| z |
| 1 |
| 2 |
∴-
| 1 |
| 2 |
| x |
| z |
| 1 |
| 2 |
| y |
| z |
故答案为:-
| 1 |
| 2 |
| y |
| z |
点评:本题主要考查了不等式的基本性质,解题的关键是确定x>0,z<0,得出-
<
<1,
| 1 |
| 2 |
| y |
| z |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列运算正确的是( )
| A、(-3)0=-1 |
| B、3-2=-6 |
| C、-30=-1 |
| D、-3-2=-9 |
 已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是( )| A、y>0 | B、y<2 |
| C、y<0 | D、-4<y<0 |
 如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.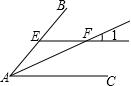 如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=25°,则∠BEF的度数为
如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=25°,则∠BEF的度数为