题目内容
4. 如同,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是( )
如同,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{AD}{AE}$=$\frac{AC}{AB}$ | C. | ∠ADE=∠C | D. | ∠AED=∠B |
分析 根据相似三角形的判定定理进行判定即可.
解答 解:∵∠DAE=∠CAB,
∴当∠AED=∠B或∠ADE=∠C时,△ABC∽△AED;
当$\frac{AD}{AC}$=$\frac{AE}{AB}$即$\frac{AD}{AE}$=$\frac{AC}{AB}$时,△ABC∽△AED.
故选:A.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
相关题目
14.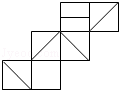 如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
 如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
如图给定的是纸盒的外表面,下面能由它折叠而成的是( )| A. | 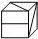 | B. | 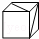 | C. |  | D. |  |
12.下列计算错误的是( )
| A. | (-2)3=-8 | B. | (-1)2016=1 | C. | (-$\frac{1}{2}$)4×(-1)3=$\frac{1}{16}$ | D. | (-3)3×(-1)4=-27 |
16.若2a=3b,则$\frac{a}{b}$=( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
3.若一个三角形三个内角度数的比为2:7:5,那么这个三角形是( )
| A. | 直角三角形 | B. | 钝角三角形 | C. | .锐角三角形 | D. | 无法确定 |
 如图,BD是∠ABC的角平分线,ED∥BC,交AB于点E,∠A=45°,∠BDC=60°,求∠ABD和∠BED的度数.
如图,BD是∠ABC的角平分线,ED∥BC,交AB于点E,∠A=45°,∠BDC=60°,求∠ABD和∠BED的度数.