题目内容
如图(1),在Rt△ABC的边AB的同侧,分别以三边为直径作三个半圆,大半圆以外的两部分面积分别为S1、S3,三角形的面积为S2;
如图(2),两个反比例函数 和
和 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象上,PC⊥x轴于点C,PD⊥y轴于点D,交
的图象上,PC⊥x轴于点C,PD⊥y轴于点D,交 的图象于分别于点A,B,当点P在
的图象于分别于点A,B,当点P在 的图象上运动时,△BOD,四边形OAPB,△AOC的面积分别为S1、S2、S3;
的图象上运动时,△BOD,四边形OAPB,△AOC的面积分别为S1、S2、S3;
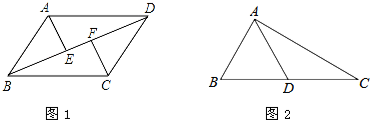
如图(3),点E为?ABCD边AD上任意一点,三个三角形的面积分别为S1、S2、S3;
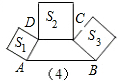
如图(4),梯形ABCD中,AB∥CD,∠DAB+∠ABC=90°,AB=2CD,以AD、DC、CB为边作三个正方形的面积分别为S1、S2、S3.
在这四个图形中满足S1+S3=S2有______(填序号).

解:(1)如图:可得S1+S3= π
π +
+ π
π +S2-
+S2- π
π =
= π(AC2+BC2-AB2)+S2,
π(AC2+BC2-AB2)+S2,
又∵AB2=AC2+BC2,
∴S1+S3=S2.
(2)根据k的几何意义可得:SBDO= |k|=
|k|= ,SAOC=
,SAOC= |k|=
|k|= ,SOAPB=2-SBDO-SAOC=1,
,SOAPB=2-SBDO-SAOC=1,
∴S1+S3=S2.
(3)根据平行四边形的性质可得S2= SABCD,
SABCD,
∴S1+S2= SABCD,
SABCD,
∴S1+S3=S2.
(4) ∵AB∥DC,
∵AB∥DC,
∴四边形DCBE是平行四边形,
∴DC=BE,BC=DE,∠ABC=∠AED,
∵∠DAB+∠ABC=90°,2DC=AB,
∴DC=AE,∠DAE+∠AED=90°,
∴∠ADE=90°那么AD2+DE2=AE2,
∵S1=AD2,S2=DC2=AE2,S3=BC2=AE2,
∴S2=S1+S3.
综上可得(1)(2)(3)(4)四个图形均满足S2=S1+S3.
故答案为(1)(2)(3)(4).
分析:图(1)根据AB2=AC2+BC2,半圆的面积等于 πr2,可得出S1、S2、S3的关系.
πr2,可得出S1、S2、S3的关系.
图(2)过双曲线上任意一点引x轴、y轴垂线,所得矩形面积S是个定值|k|,△BOD的面积为矩形面积的一半,即 |k|,从而可判断出S1、S2、S3的关系.
|k|,从而可判断出S1、S2、S3的关系.
图(3)根据平行四边形的性质可得S2= SABCD,从而可得出S1+S3=S2.
SABCD,从而可得出S1+S3=S2.
图(4)过点D作EE∥BC交AB于点E,得到平行四边形DCBE和Rt△ADE,根据平行四边形的性质和勾股定理,不难证明三个正方形的边长对应等于所得直角三角形的边.
点评:本题考查了勾股定理、反比例函数的几何意义及平行四边形的性质,涉及的知识点较多,难度较大,解答本题关键是根据反比例函数的几何意义,平心四边形的性质,梯形的知识分别表示出各图中的S1、S2、S3.
 π
π +
+ π
π +S2-
+S2- π
π =
= π(AC2+BC2-AB2)+S2,
π(AC2+BC2-AB2)+S2,又∵AB2=AC2+BC2,
∴S1+S3=S2.
(2)根据k的几何意义可得:SBDO=
 |k|=
|k|= ,SAOC=
,SAOC= |k|=
|k|= ,SOAPB=2-SBDO-SAOC=1,
,SOAPB=2-SBDO-SAOC=1,∴S1+S3=S2.
(3)根据平行四边形的性质可得S2=
 SABCD,
SABCD,∴S1+S2=
 SABCD,
SABCD,∴S1+S3=S2.
(4)
 ∵AB∥DC,
∵AB∥DC,∴四边形DCBE是平行四边形,
∴DC=BE,BC=DE,∠ABC=∠AED,
∵∠DAB+∠ABC=90°,2DC=AB,
∴DC=AE,∠DAE+∠AED=90°,
∴∠ADE=90°那么AD2+DE2=AE2,
∵S1=AD2,S2=DC2=AE2,S3=BC2=AE2,
∴S2=S1+S3.
综上可得(1)(2)(3)(4)四个图形均满足S2=S1+S3.
故答案为(1)(2)(3)(4).
分析:图(1)根据AB2=AC2+BC2,半圆的面积等于
 πr2,可得出S1、S2、S3的关系.
πr2,可得出S1、S2、S3的关系.图(2)过双曲线上任意一点引x轴、y轴垂线,所得矩形面积S是个定值|k|,△BOD的面积为矩形面积的一半,即
 |k|,从而可判断出S1、S2、S3的关系.
|k|,从而可判断出S1、S2、S3的关系.图(3)根据平行四边形的性质可得S2=
 SABCD,从而可得出S1+S3=S2.
SABCD,从而可得出S1+S3=S2.图(4)过点D作EE∥BC交AB于点E,得到平行四边形DCBE和Rt△ADE,根据平行四边形的性质和勾股定理,不难证明三个正方形的边长对应等于所得直角三角形的边.
点评:本题考查了勾股定理、反比例函数的几何意义及平行四边形的性质,涉及的知识点较多,难度较大,解答本题关键是根据反比例函数的几何意义,平心四边形的性质,梯形的知识分别表示出各图中的S1、S2、S3.

练习册系列答案
相关题目
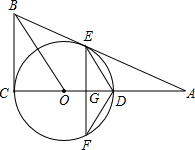 (2012•中江县二模)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,且BO∥ED,作弦EF⊥AC于G,连接DF.
(2012•中江县二模)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,且BO∥ED,作弦EF⊥AC于G,连接DF.
 如图,已知:在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D.
如图,已知:在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D. 如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.
如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.