题目内容
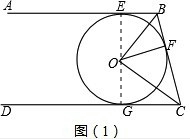
(2012•天河区一模)如图(1),AB、BC、CD分别与⊙O相切于点E、F、G,且AB∥CD,若OB=6,OC=8,
(1)求BC和OF的长;
(2)求证:E、O、G三点共线;
(3)小叶从第(1)小题的计算中发现:等式
=
+
成立,于是她得到这样的结论:
如图(2),在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,设BC=a,AC=b,CD=h,则有等式
+
=
成立.请你判断小叶的结论是否正确,若正确,请给予证明,若不正确,请说明理由.

(1)求BC和OF的长;
(2)求证:E、O、G三点共线;
(3)小叶从第(1)小题的计算中发现:等式
| 1 |
| OF2 |
| 1 |
| OB2 |
| 1 |
| OC2 |
如图(2),在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,设BC=a,AC=b,CD=h,则有等式
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |

分析:(1)根据切线的性质可得出BO,CO分别平分∠ABC,∠BCD,结合平行线的性质可得出∠BOC=90°,利用勾股定理可求出BC的长,根据△BOC面积的两种表达形式可求出OF;
(2)连接OE、OG,根据切线的性质可得∠BEO=∠BFO=90°,∠BOE=∠BOF,∠COG=∠COF,然后得出∠EOG=180°即可得出结论;
(3)由tan∠CAB=
=
,然后将等式两边平方变形即可得出结论.
(2)连接OE、OG,根据切线的性质可得∠BEO=∠BFO=90°,∠BOE=∠BOF,∠COG=∠COF,然后得出∠EOG=180°即可得出结论;
(3)由tan∠CAB=
| a |
| b |
| h | ||
|
解答:解:(1)∵AB∥CD,
∴∠ABC+∠BCD=180°,
又∵AB,BC,CD分别与⊙O相切于点E,F,G,
∴BO,CO分别平分∠ABC,∠BCD,
∴∠OBC+∠OCB=90°,
又∵在Rt△BOC中,∠BOC=90°,OB=6,OC=8,
∴BC=
=10,
∴S△BOC=
BC•OF=
BO•CO,
即:10×OF=6×8,
解得:OF=4.8.
(2)连接OE,OG,
∵BO分别平分∠ABC,
∴∠EBO=∠FBO,
又∵AB,BC分别与⊙O相切于点E,F,
∴∠BEO=∠BFO=90°,∠BOE=∠BOF,
同理:∠COG=∠COF,
∵∠OBC+∠OCB=90°,
∴∠EOG=∠EOB+∠BOF+∠COF+∠COG=180°,
∴E,O,G三点共线.
(3)等式2成立.
理由如下:
∵tan∠CAB=
=
,
∴
=
,
∴a2b2=(a2+b2)h2,
∴
=
,
即可得:
+
=
.
∴∠ABC+∠BCD=180°,
又∵AB,BC,CD分别与⊙O相切于点E,F,G,
∴BO,CO分别平分∠ABC,∠BCD,
∴∠OBC+∠OCB=90°,
又∵在Rt△BOC中,∠BOC=90°,OB=6,OC=8,
∴BC=
| OB2+OC2 |
∴S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
即:10×OF=6×8,
解得:OF=4.8.
(2)连接OE,OG,

∵BO分别平分∠ABC,
∴∠EBO=∠FBO,
又∵AB,BC分别与⊙O相切于点E,F,
∴∠BEO=∠BFO=90°,∠BOE=∠BOF,
同理:∠COG=∠COF,
∵∠OBC+∠OCB=90°,
∴∠EOG=∠EOB+∠BOF+∠COF+∠COG=180°,
∴E,O,G三点共线.
(3)等式2成立.
理由如下:
∵tan∠CAB=
| a |
| b |
| h | ||
|
∴
| a2 |
| b2 |
| h2 |
| b2-h2 |
∴a2b2=(a2+b2)h2,
∴
| a2b2 |
| a2b2h2 |
| (a2+b2)h2 |
| a2b2h2 |
即可得:
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |
点评:此题属于圆的综合题目,涉及了切线的性质、三角函数及等式的变形,第二问的关键是掌握三点一线需满足的条件,第三问的解答有一定技巧,可以通过灵活变形得出答案,也可以利用相似三角形的知识,分别表示出a2、b2、h2,从而得出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
