题目内容
 如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.
如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.分析:由∠CAD:∠DAB=1﹕2,可设∠CAD=x°,∠DAB=2x°,由E为AB的中点,且DE⊥AB于E,根据线段垂直平分线的性质,可得∠B=∠DAB=2x°,继而可得5x=90,解此方程即可求得答案.
解答:解:由题意,设∠CAD=x°,∠DAB=2x°,
∵E为AB的中点,且DE⊥AB,
∴DE为AB的中垂线,
∴AD=DB,
∴∠B=∠DAB=2x°,
∴∠B+∠CAB=2x°+3x°=5x°,
∵在Rt△ABC中,∠C=90°,
∴∠B+∠CAB=90°,
∴5x=90,
∴x=18,
∴∠B=2x°=36°.
∵E为AB的中点,且DE⊥AB,
∴DE为AB的中垂线,
∴AD=DB,
∴∠B=∠DAB=2x°,
∴∠B+∠CAB=2x°+3x°=5x°,
∵在Rt△ABC中,∠C=90°,
∴∠B+∠CAB=90°,
∴5x=90,
∴x=18,
∴∠B=2x°=36°.
点评:此题考查了线段垂直平分线的性质、等腰三角形的性质以及三角形内角和定理.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
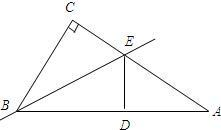 如图,已知,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合.
如图,已知,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合.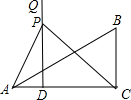 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.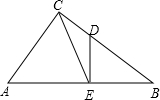 如图,已知:在Rt△ABC中,∠ACB=90°,sinB=
如图,已知:在Rt△ABC中,∠ACB=90°,sinB= 21、如图,已知:在Rt△ABC中,∠ACB=90°,AC=4,BC=3,AM=AC,BN=BC.
21、如图,已知:在Rt△ABC中,∠ACB=90°,AC=4,BC=3,AM=AC,BN=BC. 如图,已知:在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D.
如图,已知:在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D.