题目内容
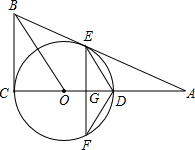（2012•中江县二模）如图，⊙O的圆心在Rt△ABC的直角边AC上，⊙O经过C、D两点，与斜边AB交于点E，连接BO、ED，且BO∥ED，作弦EF⊥AC于G，连接DF．（1）求证：AB为⊙O的切线；
（2）连接CE，求证：AE2=AD•AC；
（3）若⊙O的半径为5，sin∠DFE=
| 3 | 5 |
分析：（1）连接OE，首先证明△BCO≌△BEO，可以得到∠BEO=∠BCO=90°，即OE⊥AB，则AB是⊙O切线；
（2）证明△AED∽△ACE，利用相似三角形的对应边的比相等即可证得；
（3）首先利用勾股定理即可求得CE的长，然后利用三角函数的定义即可求解．
（2）证明△AED∽△ACE，利用相似三角形的对应边的比相等即可证得；
（3）首先利用勾股定理即可求得CE的长，然后利用三角函数的定义即可求解．
解答：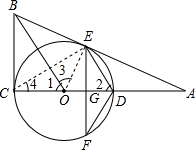
解：（1）证明：连接OE．
∵ED∥OB，∠2=∠OED，∴∠1=∠3．
又OB=OB，OE=OC，
∴△BCO≌△BEO．（SAS）
∴∠BEO=∠BCO=90°，即OE⊥AB，
∴AB是⊙O切线．
（2）连接CE．
∵∠CEO+∠OED=∠OED+∠DEA=90°，∴∠CEO=∠DEA．
又∠CEO=∠4，∴∠4=∠DEA，
又∠A=∠A，∴△AED∽△ACE．
∴
=
，∴AE2=AD•AC．
（3）∵CD为⊙O的直径，
∴∠CED=90°，CD=2CO=10．
∴ED=CD•sin∠4=CD•sin∠DFE=10×
=6．
∴CE=
=
=8．
在Rt△CEG中，
=sin∠4=
，
∴EG=
×8=
．
根据垂径定理得：EF=2EG=
．
解：（1）证明：连接OE．∵ED∥OB，∠2=∠OED，∴∠1=∠3．
又OB=OB，OE=OC，
∴△BCO≌△BEO．（SAS）
∴∠BEO=∠BCO=90°，即OE⊥AB，
∴AB是⊙O切线．
（2）连接CE．
∵∠CEO+∠OED=∠OED+∠DEA=90°，∴∠CEO=∠DEA．
又∠CEO=∠4，∴∠4=∠DEA，
又∠A=∠A，∴△AED∽△ACE．
∴
| AE |
| AC |
| AD |
| AE |
（3）∵CD为⊙O的直径，
∴∠CED=90°，CD=2CO=10．
∴ED=CD•sin∠4=CD•sin∠DFE=10×
| 3 |
| 5 |
∴CE=
| CD2-ED2 |
| 102-62 |
在Rt△CEG中，
| EG |
| CE |
| 3 |
| 5 |
∴EG=
| 3 |
| 5 |
| 24 |
| 5 |
根据垂径定理得：EF=2EG=
| 48 |
| 5 |
点评：本题考查了切线的证明，以及相似三角形的判定与性质，三角函数，证明切线常用的方法是转化成证明垂直．
练习册系列答案
习题精选系列答案
相关题目
（2012•中江县二模）如图，O是正方形ABCD的对角线AC上一点，⊙O与边BC、CD都相切，点E、F分别在AB、AD上．现将△AEF沿着EF对折，折痕EF与⊙O相切，此时点A恰好落在圆心O处．若AF=4，则四边形ABCD的边长是（ ）
（2012•中江县二模）二次函数y=ax2+bx+c（a≠0）的草图如右．下面的五个结论：①c＞1，②2a-b=0，③4ac＜b2，④abc＜0，⑤9a+3b+c＜0．其中正确的有（ ）