题目内容
3．已知3x-2y-5z=0，2x-5y+4z=0且x，y，z均不为零，求$\frac{3{x}^{2}+2{y}^{2}+5{z}^{2}}{{5}^{2}x+{y}^{2}-9{z}^{2}}$．分析 把z看做已知数表示出x与y，代入原式计算即可得到结果．
解答 解：联立得：$\left\{\begin{array}{l}{3x-2y=5z①}\\{2x-5y=-4z②}\end{array}\right.$，
①×5-②×2得：11x=33z，即x=3z，
把x=3z代入①得：y=2z，
则原式=$\frac{27{z}^{2}+8{z}^{2}+5{z}^{2}}{45{z}^{2}+4{z}^{2}-9{z}^{2}}$=1．
点评 此题考查了解三元一次方程组，熟练掌握运算法则是解本题的关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
13．弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂的物体的重量x（kg）间有下面的关系：
下列说法不正确的是（ ）
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A． | x与y都是变量，且x是自变量，y是因变量 | |
| B． | 物体质量每增加1kg，弹簧长度y增加0.5cm | |
| C． | y与x的关系表达式是y=0.5x | |
| D． | 所挂物体质量为7kg时，弹簧长度为13.5cm |
11．
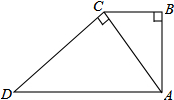如图，梯形ABCD中，AD∥BC，∠B=∠ACD=90°，AB=3，DC=5，则△ABC与△DCA的面积比为（ ）
如图，梯形ABCD中，AD∥BC，∠B=∠ACD=90°，AB=3，DC=5，则△ABC与△DCA的面积比为（ ）| A． | 2：3 | B． | 3：5 | C． | 9：25 | D． | $\sqrt{3}$：$\sqrt{5}$ |
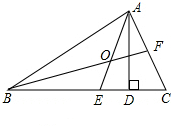已知：如图，△ABC中，AD、AE分别是△ABC的高和角平分线，BF是∠ABC的平分线，BF与AE交于O，若∠ABC=40°，∠C=60°，求∠DAE、∠BOE的度数．