题目内容
17.已知圆锥的侧面积等于60πcm2,母线长10cm,则圆锥的高是8cm.分析 设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式得到$\frac{1}{2}$•2π•r•10=60π,解得r=6,然后根据勾股定理计算圆锥的高.
解答 解:设圆锥的底面圆的半径为r,
根据题意得$\frac{1}{2}$•2π•r•10=60π,
解得r=6,
所以圆锥的高=$\sqrt{1{0}^{2}-{6}^{2}}$=8(cm).
故答案为8.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
8.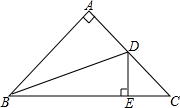 如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )
如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )
 如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )
如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )| A. | $\frac{1}{3}$ | B. | $\sqrt{2}$-1 | C. | 2-$\sqrt{3}$ | D. | $\frac{1}{4}$ |
12.下列运算正确的是( )
| A. | a+2a=3a2 | B. | 3a3•2a2=6a6 | C. | a8÷a2=a4 | D. | (2a)3=8a3 |
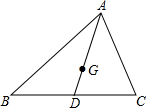 如图,AD为△ABC中线,点G为重心,若AD=6,则AG=4.
如图,AD为△ABC中线,点G为重心,若AD=6,则AG=4.