题目内容
12．
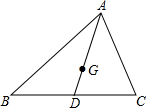如图，AD为△ABC中线，点G为重心，若AD=6，则AG=4．
分析 首先根据重心到顶点的距离与重心到对边中点的距离之比为2：1，可得AG的长度是AD的长度的$\frac{2}{2+1}=\frac{2}{3}$；然后根据分数乘法的意义，用AD的长度乘以$\frac{2}{3}$，求出AG的长度是多少即可．
解答 解：∵重心到顶点的距离与重心到对边中点的距离之比为2：1，
∴AG=AD×$\frac{2}{2+1}$
=6×$\frac{2}{3}$
=4．
故答案为：4．
点评 此题主要考查了三角形的重心，要熟练掌握，解答此题的关键是要明确：重心到顶点的距离与重心到对边中点的距离之比为2：1．
练习册系列答案
相关题目
如图，在等边三角形ABC中，点E、F分别是AB、AC的中点，EF=4，△ABC的周长为24．
一次函数y=kx+1的图象如图，则反比例函数y=$\frac{k}{x}$（x＜0）的图象只能是（ ）
4．面积为10m2的正方形地毯，它的边长介于（ ）
| A． | 2m与3m之间 | B． | 3m与4m之间 | C． | 4m与5m之间 | D． | 5m与6m之间 |
如图，抛物线y=-x2+6x交x轴正半轴于点A，顶点为M，对称轴MB交x轴于点B．过点C（2，0）作射线CD交MB于点D（D在x轴上方），OE∥CD交MB于点E，EF∥x轴交CD于点F，作直线MF．