Question

14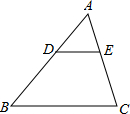．如图，D、E分别是△ABC的边AB、AC上的点，且DE∥BC，AD=2，DB=3，则△ADE与四边形BCED的面积之比是（　　）

• A． 4：21
• B． 4：9
• C． 2：5
• D． 2：3

Answer 1

分析 先判断△ADE∽△ABC，再根据相似三角形的面积之比=相似比的平方即可得到结论．

解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$，
∵AD=2，DB=3，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{2}{5}$，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{DE}{BC}$）²=$\frac{4}{25}$，
∴△ADE与四边形BCED的面积之比是$\frac{4}{21}$．
故选：A．

点评 本题考查了相似三角形的判定和性质，注意：相似三角形的面积之比=相似比的平方．