题目内容
4．
如图，等腰梯形ABCD中，AD∥BC，AB=AD=CD=4，∠B=60°，则这个等腰梯形的周长为20．
分析 作DE∥AB交BC与点E．则四边形ABED是平行四边形，△DEC是等边三角形，即可求得CD，BE的长度，从而求解．
解答 解：
作DE∥AB交BC与点E．
则四边形ABED是平行四边形，△DEC是等边三角形．
∴BE=AD=4，EC=DC=AB=4．
∴梯形ABCD的周长=AD+AB+BC+CD=AB+AD+BE+EC+CD=20．
故答案为：20．
点评 本题考查等腰梯形的有关计算，正确作出辅助线，转化成平行四边形与等边三角形是关键．
练习册系列答案
优生乐园系列答案
相关题目
18．
如图，小明课间把老师的三角板的直角顶点放在两条平行线a、b上，已知∠1=55°，则∠2的度数为（ ）
如图，小明课间把老师的三角板的直角顶点放在两条平行线a、b上，已知∠1=55°，则∠2的度数为（ ）| A． | 35° | B． | 45° | C． | 55° | D． | 75° |
为方便住校生晚自习后回到宿舍就寝，赵化中学新安装了一批照明路灯；一天上午小刚在观看新安的照明灯时，发现在太阳光的正面照射下，照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端，小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米，同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米，请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度？
20．下列说法中正确的有（ ）
①位似图形一定是相似图形；
②相似图形一定是位似图形；
③两个全等的位似图形的位似中心在两个图形之间或在这两个图形的公共边上；
④全等图形一定是位似图形，且位似比为1：1；
⑤若图形a与图形b是位似图形，图形b与图形c是位似图形，则图形a与图形c也一定是位似图形．
①位似图形一定是相似图形；
②相似图形一定是位似图形；
③两个全等的位似图形的位似中心在两个图形之间或在这两个图形的公共边上；
④全等图形一定是位似图形，且位似比为1：1；
⑤若图形a与图形b是位似图形，图形b与图形c是位似图形，则图形a与图形c也一定是位似图形．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，四边形ABCD是矩形，E是BD上的一点，∠BAE=∠BCE，∠AED=∠CED，点G是BC，AE延长线的交点，AG与CD相交于点F．
16．关于x的方程x2-2x+m2-4=0的两个根互为倒数，则m的值为（ ）
| A． | $-\sqrt{5}$ | B． | $\sqrt{5}$ | C． | $±\sqrt{5}$ | D． | ±2 |
14．
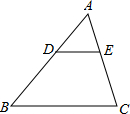如图，D、E分别是△ABC的边AB、AC上的点，且DE∥BC，AD=2，DB=3，则△ADE与四边形BCED的面积之比是（ ）
如图，D、E分别是△ABC的边AB、AC上的点，且DE∥BC，AD=2，DB=3，则△ADE与四边形BCED的面积之比是（ ）| A． | 4：21 | B． | 4：9 | C． | 2：5 | D． | 2：3 |