题目内容
3.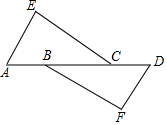 如图,AE∥DF,AB=DC,不再添加辅助线和字母,要使△EAC≌△FDB,需添加的一个条件是∠E=∠F或AE=DF(只写一个条件即可)
如图,AE∥DF,AB=DC,不再添加辅助线和字母,要使△EAC≌△FDB,需添加的一个条件是∠E=∠F或AE=DF(只写一个条件即可)
分析 添加条件AB=CD可证明AC=BD,然后再根据AE∥FD,可得∠A=∠D,再利用ASA定理证明△EAC≌△FDB即可,或AE=DF利用SAS定理证明△EAC≌△FDB.
解答 解:添加∠E=∠F,理由如下:
∵AE∥FD,
∴∠A=∠D,
∵AB=CD,
∴AC=BD,
在△AEC和△DFB中,$\left\{\begin{array}{l}{∠E=∠F}\\{AE=FD}\\{∠A=∠D}\end{array}\right.$,
∴△EAC≌△FDB(ASA).
故答案是:∠E=∠F.
当添加AE=DF时,利用SAS即可证得.
故答案是:∠E=∠F或AE=DF.
点评 此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
18.下列四个等式从左到右的变形,是多项式因式分解的是( )
| A. | (a+3)(a-3)=a2-9 | B. | x2+x-5=x(x+1)-5 | C. | x2+x=x(x+$\frac{1}{x}$) | D. | a2b+ab2=ab(a+b) |
8.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000,4400000000这个数用科学记数法表示为( )
| A. | 44×108 | B. | 4.4×108 | C. | 4.4×109 | D. | 0.44×1010 |
10.下列计算中,正确的是( )
| A. | (a+b)2=a2+b2 | B. | (x-3y)2=x2-3xy+9y2 | ||
| C. | (6a3-4a2+2a)÷2a=3a2-2a | D. | ab2÷a=b2 |
 如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,BC=12,则DE的长是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,BC=12,则DE的长是( ) 如图,AD为△ABC的中线,BE为△ABD的中线
如图,AD为△ABC的中线,BE为△ABD的中线