Question

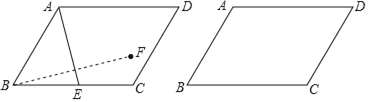
【题目】如图，点分别在两边上，且，以为直径作半圆，点是半圆的中点

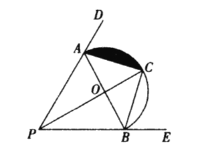
(1)连接，求证： ；

(2)若， ，求阴影部分面积

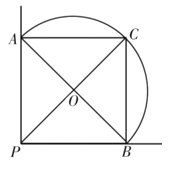
(3)若点是的外心，判断四边形的形状，并说明理由

Answer 1

【答案】（1）见解析；（2）；（3）四边形是正方形，理由见解析

【解析】

（1）求出，利用SSS即可证明；

（2）首先证明△APB是等边三角形，得到AB＝4，然后根据扇形面积公式和等腰直角三角形的面积公式计算即可；

（3）求出，证明P、O、C三点共线，可知AB⊥PC，即可得四边形是正方形．

解：（1）∵点是半圆的中点，

∴，

∴，

又∵，，

∴；

（2）∵，

∴，

∵，，

∴△APB是等边三角形，

∴AB＝PA＝4，

∴，

∴阴影部分面积；

（3）四边形是正方形，

理由：∵点是的外心，

∴，

∵，

∴，

∵PA＝PB，

∴∠AOP＝90°，

又∵，

∴P、O、C三点共线，即AB⊥PC，

∴四边形是正方形．