题目内容
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() 是
是![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
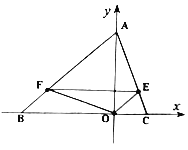
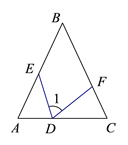
(1)如图,若点![]() 在线段
在线段![]() 上,线段
上,线段![]() 和
和![]() 之间的数量关系是 ,位置关系是 ;
之间的数量关系是 ,位置关系是 ;
(2)在(1)的条件下,当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,求证:
时,求证:![]() ;
;
(3)当点![]() 在线段
在线段![]() 的延长线上时,在线段
的延长线上时,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

【答案】(1)![]() ,
,![]() ;(2)见解析;(3)存在,
;(2)见解析;(3)存在,![]() ,理由见解析
,理由见解析
【解析】
(1)通过证△AEC≌△CMB,得到AE=CM并得到∠ACM+∠BCM=90°,进而推导出AE⊥CM;
(2)如图1,在Rt△ABC中,求得AB=12,再通过勾股定理及中位线定理,可得到FM=FG=5;
(3)将![]() 绕点
绕点![]() 逆时针旋转90°得
逆时针旋转90°得![]() ,构造全等△三角形(
,构造全等△三角形(![]() ),再证
),再证![]() ,最后在Rt△PBF中利用勾股定理得求GF,进而求得AF.
,最后在Rt△PBF中利用勾股定理得求GF,进而求得AF.
(1)![]()
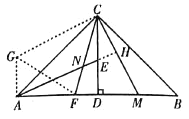
![]() 如图1,延长
如图1,延长![]() 交
交![]() 于点H.
于点H.
∵![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,
∴![]() ,
,![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() .∴
.∴![]()
∴![]() .
.
在![]() 和
和![]() 中,
中,
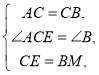 ∴
∴![]() (
(![]() ).
).
∴![]() ,
,![]() .∵
.∵![]()
∴![]() .
.
∴![]() ,∴
,∴![]() .
.
(2)解:如图1,过点![]() 作
作![]() ,且
,且![]() ,连接CG,
,连接CG,![]() ,延长
,延长![]() 交
交![]() 于点H.
于点H.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
在![]() 和△BCM中
和△BCM中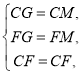
∴![]() ,
,
∴![]() .
.
由(1),知![]() , ∴
, ∴![]() ,
,
∴![]() .
.
(3)解:存在.![]() .理由如下:
.理由如下:
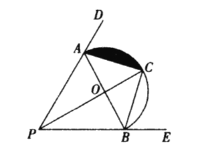
方法一:如图2,取![]() 中点
中点![]() ,连接CG并延长交
,连接CG并延长交![]() 于点H,将
于点H,将![]() 绕点
绕点![]() 逆时针旋转90°得
逆时针旋转90°得![]() ,连接
,连接![]() ,则
,则![]() .可证
.可证![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
由旋转,知![]() ,∴
,∴![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,∴,
,∴,
∴![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
在Rt△PBF中,![]() ,解得
,解得![]() .
.
∴![]() .
.
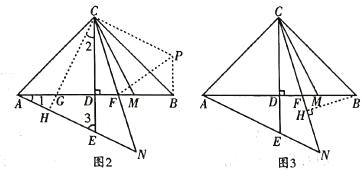
方法二:如图3,作![]() 于点H.
于点H.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,∴DE=3.
,∴DE=3.
在Rt△ADE中,由勾股定理,得![]() ,
,
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() .
.
设![]() ,则
,则![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得
![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即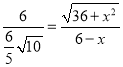 ,
,
解得![]() ,
,![]() (舍去).
(舍去).
∴![]() .∴
.∴![]() .
.

练习册系列答案
相关题目