题目内容
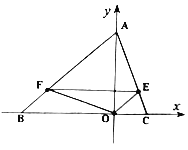
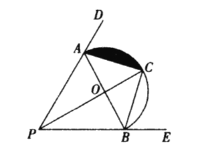
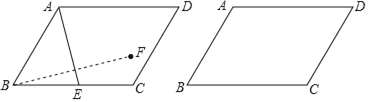
【题目】如图，已知ABCD中，∠ABC＝60°，AB＝4，BC＝m，E为BC边上的动点，连结AE，作点B关于直线AE的对称点F．
（1）若m＝6，①当点F恰好落在∠BCD的平分线上时，求BE的长；
②当E、C重合时，求点F到直线BC的距离；
（2）当点F到直线BC的距离d满足条件：2
﹣2≤d≤2+4，求m的取值范围．
【答案】（1）①BE＝10﹣2
；②
；（2）4
﹣4≤m≤8+4
【解析】
（1）①过F作FT⊥BC于T，延长BA交∠BCD的平分线于G，连接BF，EF，AF，由平行四边形性质可得：△BCG，△CDH均为等边三角形，AG=AH=2，再由B、F关于直线AE对称，可证得：△CEF∽△GFA，再结合勾股定理可求得BE的长；
②设BF交AC于T，过T作TR⊥BC于R，过F作FH⊥BC于H，过A作AG⊥BC于G，可求得BG、AG、GH、AC，再由面积法可求得BT、BF，再证明△BTR∽△BFH，结合勾股定理即可求得点F到直线BC的距离；
（2）先找出d的最大值的情形，画出图形，由d的最大值可求得m的最大值再根据d的最小值求得m的最小值，即可得m的范围．
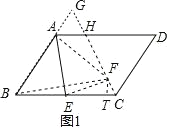
解：（1）①如图1，过F作FT⊥BC于T，延长BA交∠BCD的平分线于G，连接BF，EF，AF，
∵ABCD，
∴AB∥CD，AD∥BC，AB＝CD，AD＝BC，
∵∠ABC＝60°，
∴∠BCD＝120°，∠ADC＝60°，
∵CG平分∠BCD，
∴∠BCG＝∠DCG＝60°
∴△BCG，△CDH均为等边三角形，
∴CG＝BC＝BG＝6，∠G＝60°，DH＝CD＝4，
∴AG＝AH＝2，
∵B、F关于直线AE对称，
∴AF＝AB＝4，EF＝BE，∠AFE＝∠ABC＝60°，
∴∠AFG+∠CFE＝120°，∠AFG+∠FAG＝120°，
∴∠CFE＝∠FAG，
∴△CEF∽△GFA，
∴
，即：CF＝
EF，设BE＝EF＝x，则CF＝x，
∵∠CFT＝30°，
∴CT＝CF＝
x，FT＝
x，
∵ET2+FT2＝EF2，
∴
，
解得：x1＝10+ 
（不符合题意，舍去），x2＝10﹣，
∴BE＝10﹣2，
②如图2，设BF交AC于T，过T作TR⊥BC于R，过F作FH⊥BC于H，过A作AG⊥BC于G，连接AF，FC，
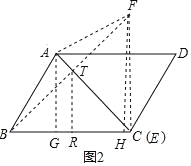
∵∠AGB＝90°，∠ABC＝60°，
∴∠BAG＝30°
∴BG＝ AB＝2，AG＝2，GC＝BC﹣BG＝4，
∴AC＝
，
∵B、F关于AC对称，
∴BF⊥AC，BT＝TF，
由△ABC面积公式可得BTAC＝AGBC，
即BT
＝2×6，
∴BT＝
，BF＝
，
在Rt△BCT中，CT＝
，
∵TRBC＝BTCT，即6TR＝
，
∴TR＝
，
∵TR⊥BC，FH⊥BC，
∴TR∥FH，
∴△BTR∽△BFH，
∴
，
∴FH＝2TR＝
，
故点F到直线BC的距离为
（2）如图3，作AG⊥BC于G，
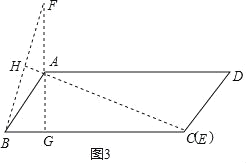
当点F、A、G三点共线时，点F到直线BC的距离d最大，
此时点E与点C重合，FG＝2 +4，
由（1）知，BG＝2，AG＝2 ，
∴BF＝
，
∴BH＝BF＝
，
∵∠BHC＝∠BGF＝90°，∠CBH＝∠FBG，
∴△CBH∽△FBG，
∴
，即
，
解得：m＝8+4 
，
∴m的最大值为8+4 ，
如图4，作AG⊥BC于G，FH⊥BC于H，FR⊥AG于R，连接AF，
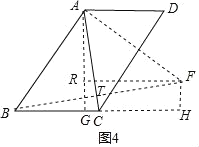
设BF交AC于T，
则AG＝2 ，BG＝2，CG＝BC﹣BG＝m-2，
此时点E与点C重合，FH＝
﹣2，
显然，FHGR是矩形，
∴RG＝FH＝﹣2， AR＝AG﹣RG＝2，
∵B、F关于AC对称，
∴BF⊥AC，BT＝TF，AF＝AB＝4，
∴RF＝GH＝
，
∴BH＝BG+GH＝2+ ，
∴BF＝
，
∴BT＝TF＝BF＝2
，
∵△BCT∽△BFH，
∴
，即
，
解得m＝4 ﹣4，
∴m的最小值为4 ﹣4，
综上所述，4﹣4≤m≤8+4．
