题目内容
在直角梯形ABCD中,AD∥BC,∠B=90°,∠BCD=60°,AD=CD.
(1)如图1,连接AC,求证:AC是∠BCD的角平分线;
(2)线段BC上一点E,将△ABE沿AE翻折,点B落到点F处,射线EF与线段CD交于点M.
①如图2,当点M与点D重合时,求证:FM=
AB;
②如图3,当点M不与点D重合时,求证:FM-DM=
AB.

(1)如图1,连接AC,求证:AC是∠BCD的角平分线;
(2)线段BC上一点E,将△ABE沿AE翻折,点B落到点F处,射线EF与线段CD交于点M.
①如图2,当点M与点D重合时,求证:FM=
| ||
| 3 |
②如图3,当点M不与点D重合时,求证:FM-DM=
| ||
| 3 |

考点:四边形综合题
专题:
分析:(1)连接AC,根据AD=CD,得出∠1=∠3,根据AD∥BC,得出∠1=∠2,进而得出答案;
(2)①过点D作DN⊥BC于点N,首先证明Rt△AFD≌Rt△DNC进而得出∠DAF=30°,即可得出答案;
②利用过点A作AG⊥CD,交CD的延长线于点G,连接AM,进而利用HL定理得出Rt△AMG≌Rt△AMF,即可得出答案.
(2)①过点D作DN⊥BC于点N,首先证明Rt△AFD≌Rt△DNC进而得出∠DAF=30°,即可得出答案;
②利用过点A作AG⊥CD,交CD的延长线于点G,连接AM,进而利用HL定理得出Rt△AMG≌Rt△AMF,即可得出答案.
解答: (1)证明:连接AC,
(1)证明:连接AC,
∵AD=CD,
∴∠1=∠3,
∵AD∥BC,
∴∠1=∠2,
∴∠2=∠3,
∴AC是∠BCD的角平分线;
(2)解:①过点D作DN⊥BC于点N,
由题意可得出:AB=DN,
∵将△ABE沿AE翻折,点B落到点F处,
∴∠B=∠AFE,AB=AF,
∴AF=DN,
在Rt△AFD和Rt△DNC中,
,
∴Rt△AFD≌Rt△DNC(HL),
∴∠1=∠C=60°,
∴∠DAF=30°,
∴
=tan30°=
,
∴FM=
AF,
∴FM=
AB;
②过点A作AG⊥CD,交CD的延长线于点G,连接AM
∵AD∥BC,
∴∠ACB=∠DAC,
∵AD=CD,
∴∠ACD=∠DAC
∴∠ACB=∠ACD,
∴AG=AB
∵AB=AF,
∴AG=AF
又∵AM=AM,
在Rt△AMG和Rt△AMF中,
∴Rt△AMG≌Rt△AMF(HL),
∴FM=GM,
∴FM一DM=GD,
∵∠ADG=∠BCD=60°
∴DG=
AG,
∴FM-DM=
AB.
 (1)证明:连接AC,
(1)证明:连接AC,∵AD=CD,
∴∠1=∠3,
∵AD∥BC,
∴∠1=∠2,
∴∠2=∠3,
∴AC是∠BCD的角平分线;
(2)解:①过点D作DN⊥BC于点N,
由题意可得出:AB=DN,
∵将△ABE沿AE翻折,点B落到点F处,
∴∠B=∠AFE,AB=AF,
∴AF=DN,
在Rt△AFD和Rt△DNC中,
|
∴Rt△AFD≌Rt△DNC(HL),
∴∠1=∠C=60°,
∴∠DAF=30°,
∴
| DF |
| AF |
| ||
| 3 |
∴FM=
| ||
| 3 |
∴FM=
| ||
| 3 |
②过点A作AG⊥CD,交CD的延长线于点G,连接AM
∵AD∥BC,
∴∠ACB=∠DAC,
∵AD=CD,
∴∠ACD=∠DAC
∴∠ACB=∠ACD,
∴AG=AB
∵AB=AF,
∴AG=AF
又∵AM=AM,
在Rt△AMG和Rt△AMF中,
|
∴Rt△AMG≌Rt△AMF(HL),
∴FM=GM,
∴FM一DM=GD,
∵∠ADG=∠BCD=60°
∴DG=
| ||
| 3 |
∴FM-DM=
| ||
| 3 |
点评:此题主要考查了翻折变换的性质以及全等三角形的判定等知识,根据已知得出全等三角形进而得出对应角对应边的关系是解题关键.

练习册系列答案
相关题目
下列式子去括号正确的是( )
| A、-(2x-y)=-2x-y |
| B、-3a2+(4a2+2)=-3a+4a2-2 |
| C、-[-(2a-3y)]=2a-3y |
| D、-3(a-7)=-3a+7 |
 如图,AB∥CD,BD平分∠ABC,若∠D=40°,则∠DCB的度数是( )
如图,AB∥CD,BD平分∠ABC,若∠D=40°,则∠DCB的度数是( )| A、100° | B、110° |
| C、120° | D、130° |
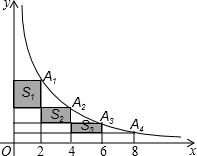 在反比例函数y=
在反比例函数y=
 如图,二次函数y=ax2+bx-3的图象与x轴交于B、C两点(点B在点C的左侧),一次函数y=mx+n的图象经过点B和二次函数图象上另一点A,点A的坐标(4,3),
如图,二次函数y=ax2+bx-3的图象与x轴交于B、C两点(点B在点C的左侧),一次函数y=mx+n的图象经过点B和二次函数图象上另一点A,点A的坐标(4,3),