Question

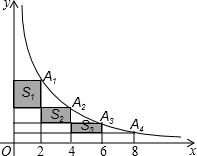在反比例函数y=

12

x

（x＞0）的图象上，有一系列点A₁，A₂，A₃，…，A_n，A_n+1，若A₁的横坐标为2，以后每个点的横坐标与它前一个点的横坐标的差都为2，过A₁，A₂，A₃，…，A_n，A_n+1分别作x轴与y轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分面积从左到右依次记为S₁，S₂，S₃，…，S_n，则S₁=

 

，S₁+S₂+S₃+…+S_n=

 

．

Answer 1

考点：反比例函数系数k的几何意义

专题：

分析：由已知条件横坐标成等差数列，再根据点A₁、A₂、A₃、…、A_n、A_n+1在反比例函数上，求出各点坐标，再由面积公式求出S_n的表达式，把n=1代入求得S₁的值．

解答：解：∵点A₁、A₂、A₃、…、A_n、A_n+1在反比例函数y=

12

x

（x＞0）的图象上，且每点的横坐标与它前一个点的横坐标的差都为2，
又点A₁的横坐标为2，
∴A₁（2，6），A₂（4，3），
∴S₁=2×（6-3）=6；
由题图象知，A_n（2n，

6

n

），A_n+1（2n+2，

6

n+1

），
∴S₂=2×（3-2）=2，
∴图中阴影部分的面积知：S_n=2×（

6

n

-

6

n+1

）=

12

n(n+1)

，（n=1，2，3，…）
∵

1

n(n+1)

=

1

n

-

1

n+1

，
∴S₁+S₂+S₃+…+S_n=12（

1

2

+

1

6

+…+

1

n(n+1)

）=12（1-

1

2

+

1

2

-

1

3

+…+

1

n

-

1

n+1

）=

12n

n+1

．
故答案为：6，

12n

n+1

．

点评：此题是一道规律题，首先根据反比例函数的性质及图象，求出A_n的坐标的表达式，再由此求出S_n的表达式．