题目内容
12. 定义:若抛物线y=ax2+bx+c与x轴的两个交点和顶点构成直角三角形,则称这条抛物线为“勾股抛物线”.
定义:若抛物线y=ax2+bx+c与x轴的两个交点和顶点构成直角三角形,则称这条抛物线为“勾股抛物线”.(1)下列抛物线:①y=x2-2x;②y=-x2-6x-8;③y=x2-4x+2是勾股抛物线的有①②(填序号).
(2)①观察你得到的勾股解析式,试猜想,在勾股抛物线y=ax2+bx+c中,b2-4ac=4(不必证明);
②若y=x2+4x+c是勾股抛物线,求c的值;
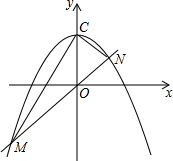
(3)如图,勾股抛物线y=-x2+1交y轴于点C,现有一直线绕O点旋转,在旋转过程中,始终保持与抛物线交M、N两点(M在N的左侧)试判断△MCN的形状,并证明你的结论.
分析 (1)设抛物线与x轴的两个交点为A、B,顶点为C.只需求出点A、B、C的坐标,再运用勾股定理的逆定理加以验证即可;
(2)①只需计算①、②两个勾股解析式对应的b2-4ac,就可给出猜想;
②只需利用①中的猜想就可求出c;
(3)设点M(x1,y1),N(x2,y2),则x1,x2分别是方程kx=-x2+1即x2+kx-1=0的两根,根据根与系数的关系可得x1+x2=-k,x1x2=-1,由y=-x2+1可得点C(0,1),由点M、N在直线y=kx上可得M(x1,kx1),N(x2,kx2),然后只需运用勾股定理及其逆定理就可解决问题.
解答 解:(1)设抛物线与x轴的两个交点为A、B,顶点为C.
①令y=0,得x2-2x=0,
解得x1=0,x2=2,
∴A(0,0),B(2,0),AB=2.
由y=x2-2x=(x-1)2-1得顶点C(1,-1),
∴AC=BC=$\sqrt{2}$,
∴AC2+BC2=4=AB2,
∴△ABC是直角三角形.
②令y=0,得-x2-6x-8=0,
解得x1=-4.x2=-2,
∴A(-4,0),B(-2,0),AB=2.
由y=-x2-6x-8=-(x+3)2+1得顶点C(-3,1),
∴AC=BC=$\sqrt{2}$,
∴AC2+BC2=4=AB2,
∴△ABC是直角三角形.
③令y=0,得x2-4x+2=0,
解得x1=2-$\sqrt{2}$,x2=2+$\sqrt{2}$,
∴A(2-$\sqrt{2}$,0),B(2+$\sqrt{2}$,0),AB=2$\sqrt{2}$.
由y=x2-4x+2=(x-2)2-2得顶点C(2,-2),
∴AC=BC=$\sqrt{(\sqrt{2})^{2}+{2}^{2}}$=$\sqrt{6}$,
∴AC2+BC2=12≠AB2,
∴△ABC不是直角三角形.
故答案为①②;
(2)①对于抛物线y=x2-2x,有b2-4ac=(-2)2-0=4;
②对于抛物线y=-x2-6x-8,有b2-4ac=(-6)2-4×(-1)×(-8)=4.
故猜想:b2-4ac=4,
故答案为4;
②由①可知b2-4ac=4,
∴16-4c=4,
∴c=3;
(3)设点M(x1,y1),N(x2,y2),
则x1,x2分别是方程kx=-x2+1即x2+kx-1=0的两根,
则有x1+x2=-k,x1x2=-1.
由y=-x2+1可得点C(0,1),
∵点M、N在直线y=kx上,
∴M(x1,kx1),N(x2,kx2),
∴MN2=(x1-x2)2+k2(x1-x2)2
=(1+k2)[(x1+x2)2-4x1x2]
=(1+k2)(k2+4)
=k4+5k2+4,
MC2+CN2=x12+(kx1-1)2+x22+(kx2-1)2
=x12+k2x12-2kx1+1+x22+k2x22-2kx2+1
=(1+k2)(x12+x22)-2k(x1+x2)+2
=(1+k2)(k2+2)-2k•(-k)+2
=k4+5k2+4,
∴MN2=MC2+CN2,
∴△MCN为直角三角形.
点评 本题主要考查了直线与抛物线的交点问题、根与系数的关系、根的判别式、完全平方公式、勾股定理及其逆定理、解一元二次方程等知识,运用勾股定理的逆定理是解决本题的关键.

| A. | $\sqrt{7}$ | B. | $\frac{22}{7}$ | C. | $\frac{π}{2}$ | D. | 0.151151115… |
某班数学兴趣小组10名同学的年龄情况如下表:
年龄(岁) | 12 | 13 | 14 | 15 |
人数 | 1 | 4 | 4 | 1 |
则这10名同学年龄的平均数和中位数分别是( )
A. 13.5,13.5 B. 13.5,13 C. 13,13.5 D. 13,14
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
| A. | 0和1之间 | B. | 1和2之间 | C. | 2和3之间 | D. | 3和4之间 |
 如图,把一个长方形纸条ABCD沿EF折叠,若∠1=55°,则∠AEG=70.
如图,把一个长方形纸条ABCD沿EF折叠,若∠1=55°,则∠AEG=70.