题目内容
8.如图1,已知∠ABC=90°,D是直线AB上的一点,AD=BC,连结DC.以CD为边,在∠CDB的同侧作∠CDE,使得∠CDE=∠ABC,并截取DE=CD,连结AE.(1)求证:△BDC≌△AED;并判断AE和BC的位置,说明理由;
(2)若将题目中的条件“∠ABC=90°”改成“∠ABC=x°(0<x<180)”,根据图形2
①结论“△BDC≌△AED”还成立吗?成立( 成立或不成立)
②试探索:当x45°时,直线AE⊥BC.

分析 (1)根据已知条件得到∠CBD=90°,根据全等三角形的判定定理得到Rt△BDC≌Rt△ADE,由全等三角形的性质得到∠A=∠CBD=90°,即可得到结论;
(2)①根据三角形外角的性质得∠C=∠ADE,根据全等三角形的判定定理即可得到△BDC≌△AED;②如图2,延长EA交BC于F,根据全等三角形的性质得到∠DBC=∠EAD然后根据等腰直角三角形的性质即可得到结论.
解答 解:(1)AE∥BC,
理由:∵∠CDE=∠ABC=90°,
∴∠CBD=90°,
在Rt△BDC与Rt△ADE中,
$\left\{\begin{array}{l}{AD=BC}\\{DE=DC}\end{array}\right.$,
∴Rt△BDC≌Rt△ADE,
∴∠A=∠CBD=90°,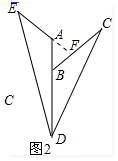
∴AE∥BC;
(2)①成立,∵∠CDE=∠ABC=x°,
∴∠C+∠CDB=∠ADE+∠CDB=x°,
∴∠C=∠ADE,
在△BDC与△AED中,
$\left\{\begin{array}{l}{BC=AD}\\{∠C=∠ADE}\\{DC=DE}\end{array}\right.$,
∴△BDC≌△AED,
故答案为:成立;
②如图2,延长EA交BC于F,
∵△BDC≌△AED,
∴∠DBC=∠EAD,
∴∠FAB=∠ABF,
∴当AE⊥BC时,
即∠AFB=90°,
∴∠FAB+∠ABF=90°,
∴∠ABC=45°,
∴当x=45时,AE⊥BC,
故答案为:45°.
点评 本题考查了全等三角形的判定和性质,平行线的判定,等腰直角三角形的性质熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 如图,DE为⊙O的直径,A为ED的延长线上一点,过点A的一条直线交⊙O于B,C两点,已知AB=OC,∠COE=78°,求∠A的度数.
如图,DE为⊙O的直径,A为ED的延长线上一点,过点A的一条直线交⊙O于B,C两点,已知AB=OC,∠COE=78°,求∠A的度数. 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,P是$\widehat{EF}$上的一点,若∠A=70°,求∠BOC、∠EPF的度数.
如图,⊙O是△ABC的内切圆,切点分别为D、E、F,P是$\widehat{EF}$上的一点,若∠A=70°,求∠BOC、∠EPF的度数. 如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,求⊙O的直径.
如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,求⊙O的直径.