题目内容
某商店用4000元购进A、B两种商品,销售完后共获利1500元,其进价和售价如下表:(获利=售价-进价)
(1)该商店购进A、B两种商品各多少件?
(2)商店第二次以原进价购进A、B两种商品,购进A种商品的件数不变,而购进B种商品的件数是第一次的2倍,A种商品按原售价销售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利2000元,则B种商品应打几折销售?
| A | B | |
| 进价(元/件) | 12 | 7 |
| 售价(元/件) | 15 | 10 |
(2)商店第二次以原进价购进A、B两种商品,购进A种商品的件数不变,而购进B种商品的件数是第一次的2倍,A种商品按原售价销售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利2000元,则B种商品应打几折销售?
考点:二元一次方程组的应用
专题:
分析:(1)设该商店购进A、B两种商品各x件、y件,根据总共花费4000元获利1500元,列方程组求解;
(2)设B种商品应打a折销售,根据第二次经营活动获利2000元,列方程求解.
(2)设B种商品应打a折销售,根据第二次经营活动获利2000元,列方程求解.
解答:解:(1)设该商店购进A、B两种商品各x件、y件,
由题意得,
,
解得:
.
答:该商店购进A、B两种商品分别是100件、400件;
(2)设B种商品应打a折销售,则
100×3+2×400(10a-7)=2000,
解得:a=0.9125,
答:B商品打9.125折出售.
由题意得,
|
解得:
|
答:该商店购进A、B两种商品分别是100件、400件;
(2)设B种商品应打a折销售,则
100×3+2×400(10a-7)=2000,
解得:a=0.9125,
答:B商品打9.125折出售.
点评:本题考查了二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.

练习册系列答案
相关题目
已知实数a、b、c满足a<0,4a-2b+c>0,则一定有( )
| A、b2-4ac>0 |
| B、b2-4ac<0 |
| C、b2-4ac≥0 |
| D、b2-4ac≤0 |
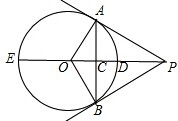 如图,PA、PB是⊙O的两条切线,点A、B为切点,直线OP交⊙O于点D、E,交AB于点C.
如图,PA、PB是⊙O的两条切线,点A、B为切点,直线OP交⊙O于点D、E,交AB于点C. 如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题: