题目内容
16.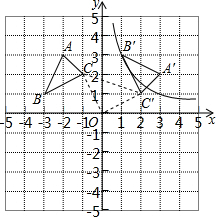 △ABC的顶点坐标为A(-2,3)、B(-3,1)、C(-1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.
△ABC的顶点坐标为A(-2,3)、B(-3,1)、C(-1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.
分析 (1)据图形旋转方向以及旋转中心和旋转角度得出对应点,根据待定系数法,即可求出解.
(2)根据勾股定理求得OC,然后根据旋转的旋转求得OC′,最后根据勾股定理即可求得.
解答 解:(1)如图所示:由图知B点的坐标为(-3,1),根据旋转中心O,旋转方向顺时针,旋转角度90°,
点B的对应点B′的坐标为(1,3),
设过点B′的反比例函数解析式为y=$\frac{k}{x}$,
∴k=3×1=3,
∴过点B′的反比例函数解析式为y=$\frac{3}{x}$.
(2)∵C(-1,2),
∴OC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵△ABC以坐标原点O为旋转中心,顺时针旋转90°,
∴OC′=OC=$\sqrt{5}$,
∴CC′=$\sqrt{O{C}^{2}+OC{′}^{2}}$=$\sqrt{10}$.
点评 本题考查了图形的旋转、勾股定理的应用以及待定系数法求反比例函数的解析式,抓住旋转的三要素:旋转中心,旋转方向,旋转角度是解题关键.

练习册系列答案
相关题目
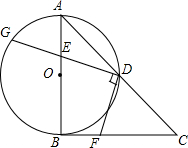 如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.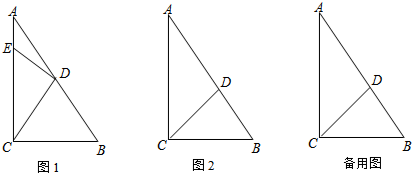
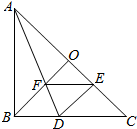 如图,在Rt△ABC中,AB=CB,BO⊥AC,DA平分∠BAC,DE⊥AC,连接EF,下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,DA平分∠BAC,DE⊥AC,连接EF,下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )