题目内容
11.解方程组(1)$\left\{\begin{array}{l}x+2y=1\\ 3x-2y=11\end{array}\right.$
(2)$\left\{\begin{array}{l}\frac{2}{3}x-\frac{3}{4}y=\frac{1}{2}\\ 4(x-y)-3(2x+y)=17\end{array}\right.$.
分析 (1)利用加减消元法解方程组即可;
(2)利用加减消元法解方程组即可.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=1①}\\{3x-2y=11②}\end{array}\right.$
①+②得:4x=12
x=3,
把x=3代入①得:3+2y=1,
解得:y=1,
∴方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$.
(2)整理方程组得:$\left\{\begin{array}{l}{8x-9y=6①}\\{2x+7y=-17②}\end{array}\right.$
②×4得:8x+28y=-68③,
③-①得:37y=-74,
y=-2,
把y=-2代入①得:8x+18=6,
x=-$\frac{3}{2}$.
∴方程组的解为:$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=-2}\end{array}\right.$.
点评 本题考查了解二元一次方程组,解决本题的关键是利用加减消元法解方程组.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
6. 如图,一次函数y=kx-2的图象与x轴交于点A,与反比例函数y=$\frac{5}{x}$(x>0)的图象交于点B,BC垂直x轴于点C,若△ABC的面积为$\frac{3}{2}$,则k的值是3.
如图,一次函数y=kx-2的图象与x轴交于点A,与反比例函数y=$\frac{5}{x}$(x>0)的图象交于点B,BC垂直x轴于点C,若△ABC的面积为$\frac{3}{2}$,则k的值是3.
 如图,一次函数y=kx-2的图象与x轴交于点A,与反比例函数y=$\frac{5}{x}$(x>0)的图象交于点B,BC垂直x轴于点C,若△ABC的面积为$\frac{3}{2}$,则k的值是3.
如图,一次函数y=kx-2的图象与x轴交于点A,与反比例函数y=$\frac{5}{x}$(x>0)的图象交于点B,BC垂直x轴于点C,若△ABC的面积为$\frac{3}{2}$,则k的值是3.
20.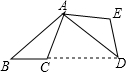 如图,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转,得到△ADE,点D恰好落在直线BC上,则旋转角的度数为( )
如图,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转,得到△ADE,点D恰好落在直线BC上,则旋转角的度数为( )
 如图,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转,得到△ADE,点D恰好落在直线BC上,则旋转角的度数为( )
如图,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转,得到△ADE,点D恰好落在直线BC上,则旋转角的度数为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
 在如图所示的网格中,每个小正方形的边长都为1.
在如图所示的网格中,每个小正方形的边长都为1. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{k^2}{x}$(x>0,k<0)的图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,则k的值是-3.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{k^2}{x}$(x>0,k<0)的图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,则k的值是-3. 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3分别与x轴、y轴交于点A,点B,点P在射线BA上(点P不与点A、B重合),过点P分别作PC⊥y轴于点C,PD⊥x轴于点D,设四边形PCOD的周长为d,点P的横坐标是m.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3分别与x轴、y轴交于点A,点B,点P在射线BA上(点P不与点A、B重合),过点P分别作PC⊥y轴于点C,PD⊥x轴于点D,设四边形PCOD的周长为d,点P的横坐标是m.