题目内容
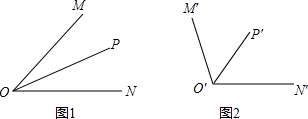
 如图,在△ABC中,∠ABC=40°,∠BAC=80°,将△ABC绕点B按逆时针方向旋转一定的角度后得到△DBE,点A恰好落在线段DE上,BE与AC相交于点F.
如图,在△ABC中,∠ABC=40°,∠BAC=80°,将△ABC绕点B按逆时针方向旋转一定的角度后得到△DBE,点A恰好落在线段DE上,BE与AC相交于点F.(1)△ABD是怎样的三角形?
(2)旋转的角度是多少?
(3)∠AFB的度数是多少?
考点:旋转的性质
专题:
分析:(1)由旋转变换的性质得到AB=DB,故△ABD是等腰三角形.
(2)由旋转变换的性质得到∠D=∠BAC=80°;由AB=DB,得到∠D=∠BAD=80°,运用三角形的内角和定理即可解决问题.
(3)求出∠ABF=20°,运用三角形的内角和定理,求出∠AFB即可解决问题.
(2)由旋转变换的性质得到∠D=∠BAC=80°;由AB=DB,得到∠D=∠BAD=80°,运用三角形的内角和定理即可解决问题.
(3)求出∠ABF=20°,运用三角形的内角和定理,求出∠AFB即可解决问题.
解答: 解:(1)如图,由旋转变换的性质得:
解:(1)如图,由旋转变换的性质得:
AB=DB,故△ABD是等腰三角形.
(2)由旋转变换的性质得:
∠D=∠BAC=80°;而AB=DB,
∴∠D=∠BAD=80°,
∴∠ABD=180°-160°=20°,
即旋转的角度是20°.
(3)∠DBE=∠ABC=40°,
故∠ABF=40°-20°=20°,
∴∠AFB=180°-80°-20°=80°.
 解:(1)如图,由旋转变换的性质得:
解:(1)如图,由旋转变换的性质得:AB=DB,故△ABD是等腰三角形.
(2)由旋转变换的性质得:
∠D=∠BAC=80°;而AB=DB,
∴∠D=∠BAD=80°,
∴∠ABD=180°-160°=20°,
即旋转的角度是20°.
(3)∠DBE=∠ABC=40°,
故∠ABF=40°-20°=20°,
∴∠AFB=180°-80°-20°=80°.
点评:该题主要考查了旋转变换的性质、三角形的内角和定理及其应用问题;解题的关键是灵活运用旋转变换的性质、三角形的内角和定理等几何知识点来推理、解答.

练习册系列答案
相关题目
下列说法不正确的是( )
| A、三角形的重心是其三条中线的交点 |
| B、三角形的三条角平分线一定交于一点 |
| C、三角形的三条高线一定交于一点 |
| D、任意一个等腰三角形都具有”三线合一“的性质 |
下列调查问题中适合采用普查方式的是( )
| A、了解2015年1月16日浙江卫视“奔跑吧兄弟”节目收视率 |
| B、了解李湾水库中鱼的平均重量 |
| C、了解新密市民对新密幸福指数第一的认可度 |
| D、了解七年级一班女生的体重 |
某反比例函数的图象过点(1,-4),则此反比例函数解析式为( )
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|