题目内容
下列说法不正确的是( )
| A、三角形的重心是其三条中线的交点 |
| B、三角形的三条角平分线一定交于一点 |
| C、三角形的三条高线一定交于一点 |
| D、任意一个等腰三角形都具有”三线合一“的性质 |
考点:三角形的角平分线、中线和高,三角形的重心,等腰三角形的性质
专题:
分析:根据三角形的重心的定义判断A;根据三角形的角平分线的定义判断B;根据三角形的高的定义于性质判断C;根据等腰三角形的性质判断D.
解答:解:A、三角形的重心是其三条中线的交点,正确;
B、三角形的三条角平分线一定交于一点,正确;
C、三角形的三条高线一定交于一点,错误;
D、任意一个等腰三角形都具有”三线合一“的性质,正确.
故选C.
B、三角形的三条角平分线一定交于一点,正确;
C、三角形的三条高线一定交于一点,错误;
D、任意一个等腰三角形都具有”三线合一“的性质,正确.
故选C.
点评:本题考查了三角形的重心,三角形的角平分线、高,等腰三角形的性质.用到的知识点:
三角形的重心是三角形三边中线的交点;三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线,三角形的三条角平分线一定交于一点;从三角形的一个顶点向它的边作垂线,垂足与顶点之间的线段叫做三角形的高,锐角三角形的三条高在三角形内部,相交于三角形内一点,直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点;等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
三角形的重心是三角形三边中线的交点;三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线,三角形的三条角平分线一定交于一点;从三角形的一个顶点向它的边作垂线,垂足与顶点之间的线段叫做三角形的高,锐角三角形的三条高在三角形内部,相交于三角形内一点,直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点;等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若代数式
的值是负数,则x的取值范围是( )
| 3 |
| 5x+2 |
A、x<-
| ||
B、x<-
| ||
C、x>-
| ||
D、x>-
|
 已知图中的两个三角形全等,则∠α度数是( )
已知图中的两个三角形全等,则∠α度数是( )| A、50° | B、58° |
| C、60° | D、72° |
已知反比例函数y=
的图象经过点(2,3),则k=( )
| k |
| x |
| A、2 | B、3 | C、-6 | D、6 |
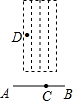 如图,田径运动会上,七年级二班的小亮同学从点C起跳,假若落地点是D,且线段CD的长度是一定的,则当AB与CD
如图,田径运动会上,七年级二班的小亮同学从点C起跳,假若落地点是D,且线段CD的长度是一定的,则当AB与CD
 如图,在△ABC中,∠ABC=40°,∠BAC=80°,将△ABC绕点B按逆时针方向旋转一定的角度后得到△DBE,点A恰好落在线段DE上,BE与AC相交于点F.
如图,在△ABC中,∠ABC=40°,∠BAC=80°,将△ABC绕点B按逆时针方向旋转一定的角度后得到△DBE,点A恰好落在线段DE上,BE与AC相交于点F.