题目内容
已知函数y=(2m-2)x+m+1,
(1)m为何值时,图象过原点.
(2)已知y随x增大而增大,求m的取值范围.
(1)m为何值时,图象过原点.
(2)已知y随x增大而增大,求m的取值范围.
考点:一次函数图象与系数的关系
专题:
分析:(1)把(0,0)代入函数解析式,列出关于系数m的方程,通过解方程求得m的值;
(2)在直线y=kx+b(k≠0)中,当k>0时,y随x的增大而增大.
(2)在直线y=kx+b(k≠0)中,当k>0时,y随x的增大而增大.
解答:解:(1)∵函数y=(2m-2)x+m+1的图象过原点,
∴m+1=0,
解得m=-1;
(2)∵y随x增大而增大,
∴2m-2>0
解得m>1.
∴m+1=0,
解得m=-1;
(2)∵y随x增大而增大,
∴2m-2>0
解得m>1.
点评:本题考查了一次函数图象与系数的关系.在直线y=kx+b(k≠0)中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.

练习册系列答案
相关题目
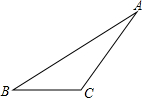 如图,在△ABC中,
如图,在△ABC中,
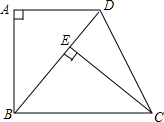 如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E. 如图是一个四边形ABCD,已知AB=DC,若再加上一个条件,就可证明它是一个平行四边形,这个条件可以是
如图是一个四边形ABCD,已知AB=DC,若再加上一个条件,就可证明它是一个平行四边形,这个条件可以是