Question

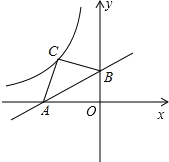
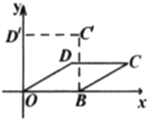
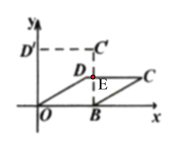
【题目】我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，将边长为4的菱形的边固定在轴上，开始时，现把菱形向左推，使点落在轴正半轴上的点处，则下列说法中错误的是（ ）

A.点的坐标为B.

C.点移动的路径长度为4个单位长度D.垂直平分

Answer 1

【答案】C

【解析】

先证明四边形OBC′D′是正方形，且边长=4，即可判断A；由平行线的性质得∠OBC的度数，进而得到，即可判断B；根据弧长公式，求出点移动的路径长度，即可判断C；证明CD⊥BC′，BC′=BC=2BE，即可判断D．

∵四边形OBCD是菱形，

∴OB=BC=CD=OD，

∴OB=BC′=C′D′=OD′，

∵∠BOD′=90°，

∴四边形OBC′D′是正方形，且边长=4，

∴点的坐标为，故A不符合题意．

∵，OD∥BC，

∴∠OBC=180°-30°=150°，

∵∠OBC′=90°，

∴，故B不符合题意．

∵点移动的路径是以OD长为半径，圆心角为∠DOD′=90°-30°=60°的弧长，

∴点移动的路径长度==，故C符合题意.

设CD与BC′交于点E，

∵在菱形OBCD中，∠C=，

∵，

∴∠BEC=180°-60°-30°=90°，即CD⊥BC′，

∴BC′=BC=2BE，

∴垂直平分，故D不符合题意．

故先C．