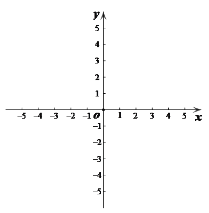题目内容
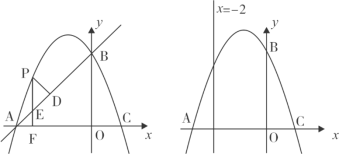
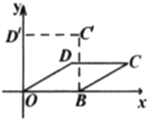
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
【答案】8
【解析】
如图,过点A作AH⊥BC于H,过点E作EM⊥AB于M,过点C作CN⊥AB于N,根据等腰三角形的性质以及三角形的面积可求出CN=4,继而根据勾股定理求出AN=3,从而求得BN的长,然后证明△EDM≌△DCN,根据全等三角形的性质可得EM=DN,设BD=x,则DN=8-x,继而根据三角形的面积公式可得S△BDE=![]() ,根据二次函数的性质即可求得答案.
,根据二次函数的性质即可求得答案.
如图,过点A作AH⊥BC于H,过点E作EM⊥AB于M,过点C作CN⊥AB于N,
∵AB=AC=5,BC=4![]() ,AH⊥BC,
,AH⊥BC,
∴BH=![]() BC=2
BC=2![]() ,
,
∴AH=![]() =
=![]() ,
,
∵S△ABC=![]() ,
,
即![]() ,
,
∴CN=4,
在Rt△CAN中,∠ANC=90°,∴AN=![]() =3,
=3,
∴BN=BA+AN=8,
∵四边形CDEF是正方形,
∴∠EDM+∠CDN=∠EDC=90°,ED=CD,
∵∠CDN+∠NCD=90°,
∴∠EDM=∠DCN,
又∵∠EMD=∠DNC=90°,
∴△EDM≌△DCN,
∴EM=DN,
设BD=x,则DN=8-x,
∴S△BDE=![]() =
=![]() =
=![]() ,
,
∵![]() ,
,
∴S△BDE的最大值为8,
故答案为:8.


【题目】有这样一个问题:探究函数y![]() x的图象与性质.
x的图象与性质.
小亮根据学习函数的经验,对函数y![]() x的图象与性质进行了探究.
x的图象与性质进行了探究.
下面是小亮的探究过程,请补充完整:
(1)函数y![]() x中自变量x的取值范围是 ;
x中自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 |
|
|
|
| 3 | 4 | 5 | 6 | … |
y | … |
|
|
| 0 |
|
|
|
| m |
|
|
| … |
求m的值;
(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)根据画出的函数图象,发现下列特征:
①该函数的图象是中心对称图形,对称中心的坐标是 ;
②该函数的图象与过点(2,0)且平行于y轴的直线越来越靠近而永不相交,该函数的图象还与直线 越来越靠近而永不相交.