题目内容
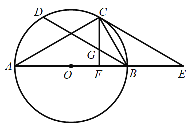
【题目】如图1,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于G,过C点的切线与射线
于G,过C点的切线与射线![]() 相交于点E,直线
相交于点E,直线![]() 与
与![]() 交于点H,
交于点H,![]() ,
,![]() .
.

(Ⅰ)求![]() 的半径;
的半径;
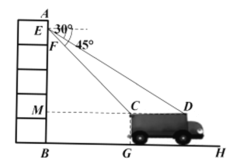
(Ⅱ)将射线![]() 绕D点逆时针旋转,得射线
绕D点逆时针旋转,得射线![]() (如图2),
(如图2),![]() 与
与![]() 交于点M,与
交于点M,与![]() 及切线
及切线![]() 分别相交于点N,F,当
分别相交于点N,F,当![]() 时,求切线
时,求切线![]() 的长.
的长.
【答案】(Ⅰ)2;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由题意连接![]() ,结合圆的切线定理和等边三角形性质以及平行线性质和同弧所对的圆心角与圆周角之间的关系进行分析求解;
,结合圆的切线定理和等边三角形性质以及平行线性质和同弧所对的圆心角与圆周角之间的关系进行分析求解;
(Ⅱ)根据题意过点F作![]() .交
.交![]() 延长线于点Q,并设
延长线于点Q,并设![]() ,则
,则![]() ,
,![]() ,利用勾股定理建立方程求解进而得出切线
,利用勾股定理建立方程求解进而得出切线![]() 的长.
的长.
解:(Ⅰ)连接![]() ,
,
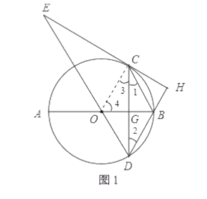
∵![]() 为
为![]() 的切线,
的切线,
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() ,
,
又∵![]()
∴![]()
∴![]() 为等边三角形
为等边三角形
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
由同弧所对的圆心角与圆周角之间的关系可知:![]()
∴![]()
∴![]()
∴![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
即![]() 的半径为2.
的半径为2.
(Ⅱ)如图2,过点F作![]() .交
.交![]() 延长线于点Q,
延长线于点Q,
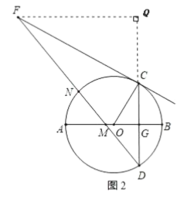
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目