题目内容
10.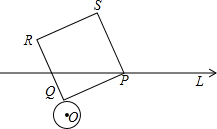 ⊙O是半径为1的圆,点O到直线L的距离为3,过直线L上的任一点P作⊙O的切线,切点为Q;若以PQ为边作正方形PQRS,则正方形PQRS的面积最小为( )
⊙O是半径为1的圆,点O到直线L的距离为3,过直线L上的任一点P作⊙O的切线,切点为Q;若以PQ为边作正方形PQRS,则正方形PQRS的面积最小为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 连结OQ、OP,作OH⊥l于H,如图,则OH=3,根据切线的性质得OQ⊥PQ,利用勾股定理得到PQ=$\sqrt{O{P}^{2}-O{Q}^{2}}$=$\sqrt{O{P}^{2}-1}$,根据垂线段最短,当OP=OH=3时,OP最小,于是PQ的最小值为2$\sqrt{2}$,即可得到正方形PQRS的面积最小值为8.
解答 解:连结OQ、OP,作OH⊥l于H,如图,则OH=3,
∵PQ为⊙O的切线,
∴OQ⊥PQ,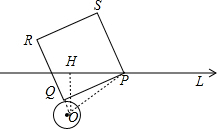
在Rt△POQ中,PQ=$\sqrt{O{P}^{2}-O{Q}^{2}}$=$\sqrt{O{P}^{2}-1}$,
当OP最小时,PQ最小,正方形PQRS的面积最小,
而当OP=OH=3时,OP最小,
所以PQ的最小值为$\sqrt{{3}^{2}-1}$=2$\sqrt{2}$,
所以正方形PQRS的面积最小值为8.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
2.已知代数式3x2-6x+3的值为9,则代数式x2-2x+6的值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 18 |
19.已知点M(a,2),B(3,b)关于y轴对称,则(a+b)2014的值( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |