题目内容
18.解下列方程(1)25x2+10x+1=10(公式法)
(2)7x2-23x+6=0.(配方法)
(3)(y+2)2=(3y-1)2(分解因式法)
(4)x2-4x-396=0(适当的方法)
分析 (1)利用求根公式进行解答;
(2)、(4)利用完全平方公式进行配方,然后直接开平方解方程即可;
(3)把右边的项移到左边,用平方差公式因式分解,求出方程的根.
解答 解:(1)由原方程,得
25x2+10x-9=0,
则a=25,b=10,c=-9,
所以△=b2-4ac=100+900=1000,
所以x=$\frac{-10±10\sqrt{10}}{50}$=$\frac{-1±\sqrt{10}}{5}$,
解得x1=$\frac{-1+\sqrt{10}}{5}$,x2=$\frac{-1-\sqrt{10}}{5}$;
(2)方程变形得:x2-$\frac{23}{7}$x=-$\frac{6}{7}$,
配方得:x2-$\frac{23}{7}$x+($\frac{23}{14}$)2=$\frac{361}{196}$,即(x-$\frac{23}{14}$)2=$\frac{361}{196}$,
开方得:x-$\frac{23}{14}$=±$\frac{19}{14}$,
解得:x1=3,x2=$\frac{2}{7}$.
(3)(y+2+3y-1)(y+2-3y+1)=0
(4y+1)(3-2y)=0
∴y1=-$\frac{1}{4}$,y2=$\frac{3}{2}$.
(4)由原方程移项,得
x2-4x=396,
等式两边同时加上一次项系数一半的平方4,得
x2-4x+4=400,
∴(x-2)2=400,
∴x=2±20,
∴x1=22,x2=-18.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
6.已知a,b,c是△ABC的三边长,且满足|a-b|+$\sqrt{c-b}$=0,则是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 不能确定 |
 如图,△ABC中,AB=41,BC=15,CA=52,AM平分∠BAC,点D、E分别为AM、AB上的动点,则BD+DE的最小值是9.
如图,△ABC中,AB=41,BC=15,CA=52,AM平分∠BAC,点D、E分别为AM、AB上的动点,则BD+DE的最小值是9. 如图,△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE分别交AC、AB于点D、E.求∠CBD的度数.
如图,△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE分别交AC、AB于点D、E.求∠CBD的度数.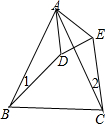 已知∠BAC=∠DAE,∠1=∠2,BD=CE.问△ABD≌△ACE吗?为什么?
已知∠BAC=∠DAE,∠1=∠2,BD=CE.问△ABD≌△ACE吗?为什么?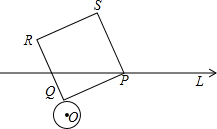 ⊙O是半径为1的圆,点O到直线L的距离为3,过直线L上的任一点P作⊙O的切线,切点为Q;若以PQ为边作正方形PQRS,则正方形PQRS的面积最小为( )
⊙O是半径为1的圆,点O到直线L的距离为3,过直线L上的任一点P作⊙O的切线,切点为Q;若以PQ为边作正方形PQRS,则正方形PQRS的面积最小为( )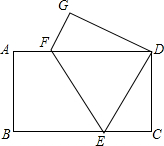 如图,长方形纸片ABCD,将纸片折叠使点A落在点G处,点B落在点D处,折痕为EF,若∠GFD:∠DFE=4:3,则∠DEC的度数为72°.
如图,长方形纸片ABCD,将纸片折叠使点A落在点G处,点B落在点D处,折痕为EF,若∠GFD:∠DFE=4:3,则∠DEC的度数为72°.