题目内容
18.抛物线y=ax2经过点(3.-1).(1)求这个二次函数的表达式;
(2)画出该二次函数的图象;
(3)当x为何值时.y值随着x值增大而增大?
分析 (1)直接把(3,-1)代入y=ax2中求出a的值即可.
(2)确定抛物线与x轴的交点坐标为(3,-1)和(-3,-1),顶点是原点,然后画图;
(3)根据图象即可求得.
解答 解:(1)把(3,-1)代入y=ax2得9a=-1,
解得a=-$\frac{1}{9}$.
所以抛物线解析式为y=-$\frac{1}{9}$x2.
(2)画出二次函数的图象如图:
(3)由图象可知:当x<0时,y值随着x值增大而增大.
点评 本题考查了待定系数法求二次函数的解析式:抛物线y=ax2,顶点坐标为(0,0);当a<0,抛物线开口向下,在对称轴左侧,y随x的增大而增大.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
11.若△ABC中,∠A=60°,且∠B:∠C=2:1,则∠B的度数为( )
| A. | 40° | B. | 80° | C. | 60° | D. | 120° |
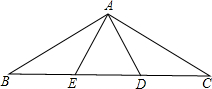 如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC.
如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC. 如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若△PMN的周长为10cm,则CD的长为10cm.
如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若△PMN的周长为10cm,则CD的长为10cm.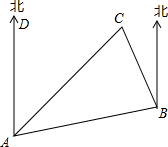 如图是A、B、C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.
如图是A、B、C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.