题目内容
 如图,已知AD=AE,要使△ABD≌△ACE,应添加的条件是
如图,已知AD=AE,要使△ABD≌△ACE,应添加的条件是考点:全等三角形的判定
专题:开放型
分析:根据“SAS”添加条件.
解答:解:∵AD=AE,
∠BAD=∠CAE,
∴当AB=AC时,可根据“SAS”判断△ABD≌△ACE.
故答案为AB=AC.
∠BAD=∠CAE,
∴当AB=AC时,可根据“SAS”判断△ABD≌△ACE.
故答案为AB=AC.
点评:本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
相关题目
 图中两个四边形是位似图形,则它们的位似中心是( )
图中两个四边形是位似图形,则它们的位似中心是( )| A、点M | B、点N | C、点O | D、点P |
“一个数x的2倍与3的和”用代数式可表示为( )
| A、2(x+3) |
| B、(2+x)x |
| C、2x+3 |
| D、2+3x |
 如图,点O为直线AB上一点,ON平分∠BOC,OM⊥ON,试说明OM平分∠AOC.
如图,点O为直线AB上一点,ON平分∠BOC,OM⊥ON,试说明OM平分∠AOC. (1)如图,AD是△ABC的中线,△ABC与△ABD的面积有怎样的数量关系?为什么?
(1)如图,AD是△ABC的中线,△ABC与△ABD的面积有怎样的数量关系?为什么? 如图是一个上下底密封纸盒(底面为正六边形)的三视图,请你根据图中数据,计算这个密封纸盒的表面积为
如图是一个上下底密封纸盒(底面为正六边形)的三视图,请你根据图中数据,计算这个密封纸盒的表面积为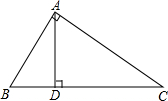 在△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=30cm,BC=50cm,求线段CD的长.
在△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=30cm,BC=50cm,求线段CD的长.