题目内容
11.在△ABC中,已知BC=2,∠B=60°,∠C=75°,求:(1)边AC的长;
(2)△ABC的面积.
分析 过点C作CD⊥BA于D,根据直角三角形的性质得到BD=1,根据勾股定理求出CD,根据等腰直角三角形的性质求出AC,根据图形计算即可.
解答 解:(1)过点C作CD⊥BA于D,
∵∠B=60°,
∴∠DCB=30°,又BC=2,
∴BD=1,
∴CD=$\sqrt{3}$,
∵∠C=75°,∠B=60°,
∴∠A=45°,又CD=$\sqrt{3}$,
∴AD=$\sqrt{3}$,
∴AC=$\sqrt{6}$;
(2)△ABC的面积=$\frac{1}{2}×\sqrt{3}×(1+\sqrt{3})=\frac{3+\sqrt{3}}{2}$.
点评 本题考查的是勾股定理的应用、直角三角形的性质,掌握直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解题的关键.

练习册系列答案
相关题目
 如图所示,在梯形ABCD中,DC∥AB,$\frac{DC}{AB}$=$\frac{1}{3}$,MN为中位线,EF∥AB且通过AC与BD的交点,点E,F分别在AD,BC上,则梯形CDEF,梯形FEMN,梯形NMAB面积的连比等于5:7:20.
如图所示,在梯形ABCD中,DC∥AB,$\frac{DC}{AB}$=$\frac{1}{3}$,MN为中位线,EF∥AB且通过AC与BD的交点,点E,F分别在AD,BC上,则梯形CDEF,梯形FEMN,梯形NMAB面积的连比等于5:7:20. 一块空地的如图如示,AB=9m、BC=12m、CD=8m、AD=17m、∠ABC=90°,求这块空地的面积.
一块空地的如图如示,AB=9m、BC=12m、CD=8m、AD=17m、∠ABC=90°,求这块空地的面积.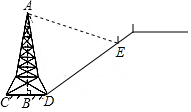 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=24 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为28.8m.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=24 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为28.8m.