题目内容
在矩形ABCD中,AB = 10,BC = 12,E为DC的中点,
连接BE,作AF⊥BE,垂足为F.
(1)求证:△BEC∽△ABF;
(2)求AF的长.
 |
(1)证明:在矩形ABCD中,有
∠C=∠ABC=∠ ABF+∠EBC=90°,
∵AF⊥BE,∴∠ AFB =∠ C=90°-
=∠ C=90°-
∴∠ABF+∠BAF =90°
 ∴∠BAF=∠EBC
∴∠BAF=∠EBC
∴△BEC∽△ABF
(2)解:在矩形ABCD中,AB = 10,∴CD=AB=10,
∵E为DC的中点,∴CE=5,
又BC = 12,在Rt△BEC 中,由勾股定理得BE=13,
由△ABF∽△BEC得

即 
解得AF=

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
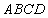 、
、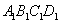 是两个边长分别为5和1且中心重合的正方形.其中,正方形
是两个边长分别为5和1且中心重合的正方形.其中,正方形 旋转,正方形
旋转,正方形 四点共线时,四边形
四点共线时,四边形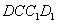 的面积为__;
的面积为__; 三点共线时,请直接写
三点共线时,请直接写 出
出 = _________;
= _________; 与直线
与直线 的位置关
的位置关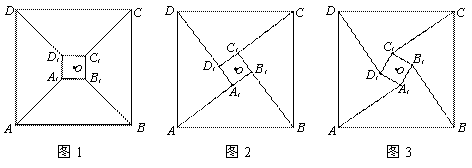
 .
. 中, ∠C=90°,分别以A、B为圆心,2为半径画圆,则图中阴影部分的面积和为
中, ∠C=90°,分别以A、B为圆心,2为半径画圆,则图中阴影部分的面积和为

 ,求代数式
,求代数式 的值.
的值.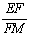 =_______;
=_______;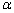 角(
角(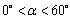 ),
),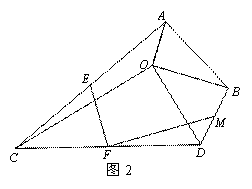 (2)如图3,若BO=
(2)如图3,若BO=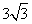 ,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
 +4x﹣5=0的两根.
+4x﹣5=0的两根.
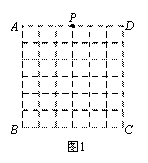
 D是一个6 × 6网格的示意图,其中每个小正方形的边长为1,位于AD中点处的点P按图2的程序移动.
D是一个6 × 6网格的示意图,其中每个小正方形的边长为1,位于AD中点处的点P按图2的程序移动.