��Ŀ����
17����֪��ABC��AB=AC����ABC=45�㣬��DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ����������ADEF��A��D��E��F����ʱ�����У�������CF����1����ͼ�٣�����D�ڱ�BC��ʱ����֤��CF+CD=$\sqrt{2}$CA��
��2����ͼ�ڣ�����D�ڱ�BC���ӳ�������������������ʱ����д��CF��CD��CA֮����ڵ�������ϵ����˵�����ɣ�
��3����ͼ�ۣ�����D�ڱ�CB���ӳ�������������������ʱ����ȫͼ�Σ���ֱ��д��CF��CD��CA֮���������ϵ��
��4������D��ֱ��BC���˶�ʱ����������������������F���˶��켣����ֱ��д��DB��DC��DA֮���������ϵ��
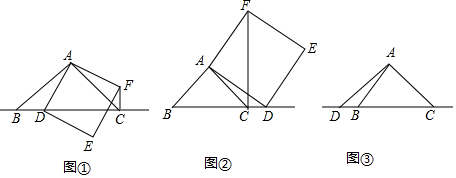
���� ��1�����ݵ���ֱ�������ε����ʵõ�BC=$\sqrt{2}$CA���������ε����ʵõ�AD=AF����DAF=90�㣬���ǵõ���BAD=��CAF=90��-��DAC������ȫ�������ε����ʼ��ɵõ����ۣ�
��2��������ǵ����ʵõ���BAD=��CAF������ȫ�������ε����ʼ��ɵõ����ۣ�
��3������ͬ��1����2����
��4������D��ֱ��BC���˶�ʱ����F���˶��켣�ǹ���C�Ҵ�ֱ��BC��ֱ�ߣ����ݹ��ɶ����õ�DF=$\sqrt{2}$AD�����ݹ��ɶ������ɵõ����ۣ�
��� ��1��֤������AB=AC����ABC=45�㣬
���BAC=90�㣬
��BC=$\sqrt{2}$CA��
���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬
���BAD=��CAF=90��-��DAC��
�ڡ�BAD�͡�CAF�У�$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAF}\\{AD=AF}\end{array}\right.$��
���BAD�ա�CAF��
��BD=CF��
��CF+CD=BC=$\sqrt{2}$CA��
��2���⣺CF-CD=$\sqrt{2}$AC���������£�
�ߡ�BAD=90��+��CAD��
��CAF=90��+��CAD��
���BAD=��CAF��
�ڡ�BAD�͡�CAF�У�
$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAF}\\{AD=AF}\end{array}\right.$��
���BAD�ա�CAF��SAS����
��BD=CF��
��BD=BC+CD��
��CF-CD=BC=$\sqrt{2}$AC��
��3��AC��CD��CF�Ĺ�ϵ��CF=CD-$\sqrt{2}$CA��
���ɣ��루1��ͬ����֤��BAD�ա�CAF���Ӷ��ɵã�
BD=CF��
����CF=CD-$\sqrt{2}$CA��
��4������D��ֱ��BC���˶�ʱ����F���˶��켣�ǹ���C�Ҵ�ֱ��BC��ֱ�ߣ�
��������ADEF�У��Խ���DF=$\sqrt{2}$AD��
��Rt��CDF��
DF2=CD2+CF2��
�ɣ�1������2��֤��BD=CF��
��CD2+BD2=2AD2��
���� ���⿼����ȫ�������ε��ж������ʣ������ε����ʣ����ɶ�������ȷ��ʶ��ͼ���ǽ���Ĺؼ���

 ��ͼʾ������ABC��һ��P�����PAC=��PBA=��PCB�����PΪ��ABC�IJ��忨�㣮�����εIJ��忨�㣨Brocard point���Ƿ�����ѧ�Һ���ѧ�����ҿ������A��L��Crelle 1780-1855����1816���״η��֣������ķ��ֲ�δ����ʱ��������ע�⣬1875�꣬���忨�㱻һ����ѧ�����߷������ٲ��忨��Brocard 1845-1922�����·��֣����������������������⣺��֪�ڵ���ֱ��������DEF�У���EDF=90�㣬����QΪ��DEF�IJ��忨�㣬DQ=1����EQ+FQ=��������
��ͼʾ������ABC��һ��P�����PAC=��PBA=��PCB�����PΪ��ABC�IJ��忨�㣮�����εIJ��忨�㣨Brocard point���Ƿ�����ѧ�Һ���ѧ�����ҿ������A��L��Crelle 1780-1855����1816���״η��֣������ķ��ֲ�δ����ʱ��������ע�⣬1875�꣬���忨�㱻һ����ѧ�����߷������ٲ��忨��Brocard 1845-1922�����·��֣����������������������⣺��֪�ڵ���ֱ��������DEF�У���EDF=90�㣬����QΪ��DEF�IJ��忨�㣬DQ=1����EQ+FQ=��������| A�� | 5 | B�� | 4 | C�� | $3+\sqrt{2}$ | D�� | $2+\sqrt{2}$ |
| A�� | $\frac{22}{7}$ | B�� | $\frac{��}{2}$ | C�� | 2 | D�� | sin30�� |
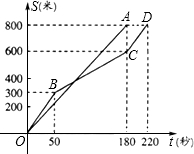 �ڽ������س���ѧҵˮƽ��������ѧ�Ƶ�Ů��800�����������У�ij����ͬʱ���ܵ�СӢ��С�����ܵ�·��S���ף�������ʱ��t���룩֮��ĺ���ͼ��ֱ�Ϊ�߶�OA������OBCD����ͼ������˵����ȷ���ǣ�������
�ڽ������س���ѧҵˮƽ��������ѧ�Ƶ�Ů��800�����������У�ij����ͬʱ���ܵ�СӢ��С�����ܵ�·��S���ף�������ʱ��t���룩֮��ĺ���ͼ��ֱ�Ϊ�߶�OA������OBCD����ͼ������˵����ȷ���ǣ�������| A�� | СӢ���ٶ���ʱ������������ | |
| B�� | С����ƽ���ٶȱ�СӢ��ƽ���ٶȴ� | |
| C�� | �����ܺ�180��ʱ���������� | |
| D�� | �����ܺ�50��ʱ��С����СӢ��ǰ�� |

| A�� | 55�� | B�� | 60�� | C�� | 65�� | D�� | 70�� |
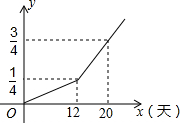 �ס����������̶ӹ�ͬ���һ��̣����ɼ�������Ȼ���ҶӼ��룬�������̶Ӻ���������¹��̣����̵Ľ���y�������ʱ��x���죩�ĺ�����ϵ��ͼ��ʾ�����Ҷӵ�����ɴ������24�죮
�ס����������̶ӹ�ͬ���һ��̣����ɼ�������Ȼ���ҶӼ��룬�������̶Ӻ���������¹��̣����̵Ľ���y�������ʱ��x���죩�ĺ�����ϵ��ͼ��ʾ�����Ҷӵ�����ɴ������24�죮