题目内容
14．关于x，y的二元一次方程组$\left\{\begin{array}{l}{4x-3y=k}\\{2x+3y=5}\end{array}\right.$的解满足x=y，则k=1．分析 将方程组用k表示出x，y，根据方程组的解满足x=y，得到关于k的方程，即可求出k的值．
解答 解：解方程组$\left\{\begin{array}{l}{4x-3y=k}\\{2x+3y=5}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{k+5}{6}}\\{y=\frac{10-k}{9}}\end{array}\right.$，
∵关于x，y的二元一次方程组$\left\{\begin{array}{l}{4x-3y=k}\\{2x+3y=5}\end{array}\right.$的解满足x=y，
∴$\frac{k+5}{6}$=$\frac{10-k}{9}$，
解得：k=1．
故答案为：1．
点评 此题考查二元一次方程组的解，掌握解方程组的方法与步骤用k表示出x，y的值是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知ABCD为正方形，∠FED=∠BEC，EF=CE，求证：DF+EF=BE．
2．在实数范围内，下列结论正确的是（ ）
| A． | 若|a|=|b|，则a=b | B． | 若a2=b2，则a=b | C． | 若$\root{3}{-a}=\root{3}{b}$，则a=-b | D． | 若a2＞b2，则a＞b |
9．若$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$是方程x-ky=0的解，则k的值为（ ）
| A． | $\frac{3}{2}$ | B． | -$\frac{3}{2}$ | C． | -$\frac{2}{3}$ | D． | $\frac{2}{3}$ |
19．把下列方程化成一般形式后，系数和为0的方程是（ ）
| A． | x2-2x+3=0 | B． | x2+2x-3=0 | C． | x2-4x-3=0 | D． | 2x2-5=3x |
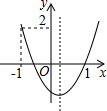如图，二次函数y=ax2+bx+c的图象开口向上，图象经过点（-1，2）和（1，0），且与y轴相交于负半轴，给出四个结论：①abc＜0；②2a+b＞0；③a+c=1；④a＞1；⑤3a+2b＜-1．其中正确结论的序号是②③④．