题目内容
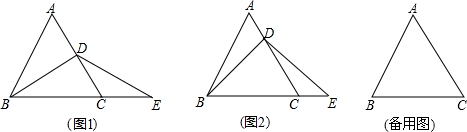
17.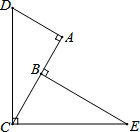 如图,已知∠DCE=∠A=90°,BE⊥AC于B,且DC=EC,BE=20cm,则AC=20cm.
如图,已知∠DCE=∠A=90°,BE⊥AC于B,且DC=EC,BE=20cm,则AC=20cm.
分析 利用同角的余角相等得到一对角相等,再由一对直角相等,CD=CE,利用AAS得到三角形ECB与三角形CDA全等,利用全等三角形对应边相等即可得到结果.
解答 证明:∵∠ECB+∠DCA=90°,∠DCA+∠D=90°,
∴∠ECB=∠D,
在△ECB和△CDA中,
$\left\{\begin{array}{l}{∠ECB=∠D}\\{∠EBC=∠A=90°}\\{CE=CD}\end{array}\right.$,
∴△ECB≌△CDA,
∴BE=AC,
∵BE=20cm,
∴AC=20cm,
故答案为:20.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
7. “六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.
“六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.
①如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次;
②假如你去转动转盘一次,获得铅笔的概率大约是0.70;
③当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
④转动转盘10次,一定有3次获得文具盒
 “六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.
“六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法正确的有①②③.①如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次;
②假如你去转动转盘一次,获得铅笔的概率大约是0.70;
③当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
④转动转盘10次,一定有3次获得文具盒
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
| 落在“铅笔”区域的频率$\frac{m}{n}$ | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
9.已知直线l平行于直线y=-2x,且过点(4,5),则l的解析式为( )
| A. | y=2x+13 | B. | y=2x-13 | C. | y=-2x+13 | D. | y=-2x-13 |
 已知:如图AB=CD,DA⊥CA,AC⊥BC.求证:△ADC≌△CBA.
已知:如图AB=CD,DA⊥CA,AC⊥BC.求证:△ADC≌△CBA.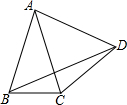 如图,△ABC中,AB=AC,∠BAC=50°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是25或100或205或310.
如图,△ABC中,AB=AC,∠BAC=50°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是25或100或205或310.