题目内容
14.比较下列各组数的大小:($\frac{5}{6}$)-0.24与($\frac{5}{6}$)${\;}^{-\frac{1}{4}}$.分析 根据指数y=ax,当a>1时,函数为增函数,当0<a<1时,函数为减函数,即可比较大小.
解答 解:根据指数y=ax,当a>1时,函数为增函数,当0<a<1时,函数为减函数,
∵0<$\frac{5}{6}$<1,
∴($\frac{5}{6}$)-0.24>($\frac{5}{6}$)${\;}^{-\frac{1}{4}}$
点评 题考查了通过指数函数的单调性比较数的大小,属于基础题,熟记指数y=ax,当a>1时,函数为增函数,当0<a<1时,函数为减函数是解决本题的关键.

练习册系列答案
相关题目
2.使分式$\frac{2-x}{(x-2){(x}^{2}-9)}$有意义的x应取( )
| A. | x≠3且x≠-3 | B. | x≠2或x≠3或x≠-3 | C. | x≠3或x≠-3 | D. | x≠2且x≠3且x≠-3 |
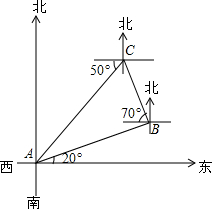 如图,一艘船由港口A出发向东偏北20°方向航行,这艘船航行的速度是每小时66海里,1小时后到达B处,发现一顶塔在西偏北79°方向,该船就朝灯塔驶去,到达灯塔后,发现港口在灯塔的西偏南50°方向,问灯塔与港口的距离是多少海里?
如图,一艘船由港口A出发向东偏北20°方向航行,这艘船航行的速度是每小时66海里,1小时后到达B处,发现一顶塔在西偏北79°方向,该船就朝灯塔驶去,到达灯塔后,发现港口在灯塔的西偏南50°方向,问灯塔与港口的距离是多少海里?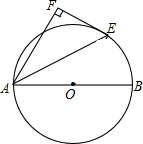 如图,AB是⊙0的直径,AE是弦,EF是⊙0的切线,E是切点,AF⊥EF,垂足为F,AE平分∠FAB吗?为什么?
如图,AB是⊙0的直径,AE是弦,EF是⊙0的切线,E是切点,AF⊥EF,垂足为F,AE平分∠FAB吗?为什么?