题目内容
16.某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,已知轿车每辆7万元,面包车每辆4万元,公司可以投入的购车款至多55万元.(1)符合公司要求的购买方案有几种?请说明理由;
(2)如果新购的10辆车每天都能租出,轿车租金为200元/日,面包车租金为110元/日,要使这10辆车的日租金不低于1500元,那么应该选择以上哪种购车方案?
分析 (1)设轿车买x辆,面包车(10-x)辆,根据购买轿车的总钱数+购买面包车的总钱数≤55万元即可得出关于x的一元一次不等式,解之即可得出x的取值范围,再结合x≥3即可确定x的取值范围,取期内的整数,此题得解;
(2)求出(1)中三种购买方案的日租金,将其与1500进行比较后即可得出结论.
解答 解:(1)设轿车买x辆,面包车(10-x)辆,
根据题意得:7x+4(10-x)≤55,
解得:x≤5.
又∵x≥3,
∴3≤x≤5,
∴x=3,4,5.
共有3种购买方案.
(2)当x=3时,10-x=7,
此时日租金为200×3+110×7=1370(元),
∵1370<1500,
∴此方案不符合题意;
当x=4时,10-x=6,
此时日租金为200×4+110×6=1460(元)
∵1460<1500,
∴此方案不符合题意;
当x=5时,10-x=5,
此时日租金为200×5+110×5=1550(元)
∵1550>1500,
∴此方案符合题意.
综上所述:要使这10辆车的日租金不低于1500元,那么应购买轿车5辆,面包车5辆.
点评 本题考查了一元一次不等式的应用,解题的关键是:(1)根据数量关系列出关于x的一元一次不等式;(2)求出三种购买方案的日租金.

练习册系列答案
相关题目
7.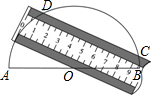 如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )
如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )
 如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )
如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )| A. | 2 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
 如图,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象相交于A(2,2),B(-1,m).
如图,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象相交于A(2,2),B(-1,m). 如图,矩形城ABCD,东边城墙AB=6km,南边城墙AD=4km,东门点E、南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=8km,HG经过A点,求FH的长.
如图,矩形城ABCD,东边城墙AB=6km,南边城墙AD=4km,东门点E、南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=8km,HG经过A点,求FH的长. 如图在△ABC和△DEF中,∠B=50°,∠A=41°,∠E=50°,∠F=89°,求证:△ABC∽△DEF.
如图在△ABC和△DEF中,∠B=50°,∠A=41°,∠E=50°,∠F=89°,求证:△ABC∽△DEF.