题目内容
9. 如图,C,D是线段AB的两个黄金分割点,AB=1,则线段CD=$\sqrt{5}$-2.
如图,C,D是线段AB的两个黄金分割点,AB=1,则线段CD=$\sqrt{5}$-2.
分析 根据黄金分割点的定义,知较短的线段=原线段的$\frac{3-\sqrt{5}}{2}$倍,可得BC的长,同理求得AD的长,则CD即可求得.
解答 解::∵线段AB=1,点C是AB黄金分割点,
∴较小线段AD=BC=1×$\frac{3-\sqrt{5}}{2}$,
则CD=AB-AD-BC=1-2×$\frac{3-\sqrt{5}}{2}$=$\sqrt{5}$-2.
故答案是:$\sqrt{5}$-2.
点评 本题考查了黄金分割,应该识记黄金分割的公式:较短的线段=原线段的$\frac{3-\sqrt{5}}{2}$倍,较长的线段=原线段的$\frac{\sqrt{5}-1}{2}$倍.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
20.若以三个数为三角形三边的长能构成直角三角形,我们就把它们称为一组勾股数,如3,4,5,勾股数之间存在一种奇妙的联系,观察下表,结合表中数的规律及相关知识,求出b,c的值
| 举例 | 猜 想 |
| 5、12、13 | 52=12+13 |
| 7、24、25 | 72=24+25 |
| … | … |
| 13、b、c | 132=b+c |
14.随着n的值变大,代数式$1+\frac{1}{n}$的值变的越来越接近于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
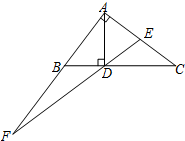 如图,△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC的中点,ED的延长线交AB的延长线于点F.若AB=5,BD=3,则$\frac{DF}{AF}$=$\frac{3}{4}$.
如图,△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC的中点,ED的延长线交AB的延长线于点F.若AB=5,BD=3,则$\frac{DF}{AF}$=$\frac{3}{4}$.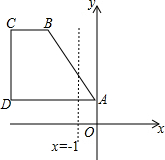 如图,已知四个点A(0,1),B(-3,4),C(-5,4),D(-5,1).
如图,已知四个点A(0,1),B(-3,4),C(-5,4),D(-5,1).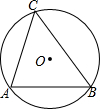 已知:如图,在△ABC中,AB=10,∠C=60°,求△ABC外接圆⊙O的半径r.
已知:如图,在△ABC中,AB=10,∠C=60°,求△ABC外接圆⊙O的半径r.