题目内容
6．
如图，点C是线段AB上的点，点D是线段BC的中点，AB=10，AC=6，则线段AD的长是（ ）| A． | 6 | B． | 2 | C． | 8 | D． | 4 |
分析 求出BC=4，由点D是线段BC的中点，得出BD=DC=$\frac{1}{2}$BC，即可得出AD的长．
解答 解：∵BC=AB-AC=4，点D是线段BC的中点，
∴CD=DB=$\frac{1}{2}$BC=2，
∴AD=AC+CD=6+2=8；
故选：C．
点评 本题考查了两点间的距离，线段中点的意义及线段的和差运算；求出CD=BD=2是解决问题的关键．
练习册系列答案
相关题目
16．若二次根式$\sqrt{3x+1}$在实数范围内有意义，则x的取值范围是（ ）
| A． | x≤-$\frac{1}{3}$ | B． | x≥-$\frac{1}{3}$ | C． | x≠-$\frac{1}{3}$ | D． | x≥0 |
17．下列各组代数式中，是同类项的为（ ）
| A． | abc2与3bac2 | B． | 2an2与-a2n | C． | 5与-2x | D． | -$\frac{1}{3}$a2y与$\frac{2}{3}$a2 |
14．已知四个点的坐标分别是（-2，2），（2，2），（2，$\frac{1}{2}$），（-2，-$\frac{1}{2}$），从中随机选一个点，在反比例函数y=$\frac{4}{x}$图象上的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{4}$ | D． | 1 |
1．已知点A（-1，0）和点B（1，2），将线段AB平移至A′B′，点A′与点A对应，若点A′的坐标为（1，-3），则点B′的坐标为（ ）
| A． | （3，0） | B． | （3，-3） | C． | （3，-1） | D． | （-1，3） |
11．已知关于x，y的方程组$\left\{\begin{array}{l}{{x}^{2}+y=25}\\{6x-y=k}\end{array}\right.$ 无实数解，则k的取值范围为k＞34．
18．甲、乙两个车站相距96千米，快车和慢车同时从甲站开出，1小时后快车在慢车前12千米，快车比慢车早40分钟到达乙站，快车和慢车的速度各是多少？设快车的速度为x千米/时，则下列方程正确的是（ ）
| A． | $\frac{96}{x}-\frac{96}{x-12}=\frac{2}{3}$ | B． | $\frac{96}{x}-\frac{96}{x-12}$=40 | C． | $\frac{96}{x-12}-\frac{96}{x}=\frac{2}{3}$ | D． | $\frac{96}{x-12}-\frac{96}{x}=40$ |
15．学校图书室整理一批图书，由一个人做要40h完成．现计划有一部分人先做4h，然后增加2人与他们一起做8h，完成这项工作．假设这些人的工作效率相同，具体应先安排多少人工作？如果设安排x人先做4h，则下列所列方程中正确的是（ ）
| A． | $\frac{4x}{40}$+$\frac{x+2}{40}$×12=1 | B． | $\frac{4x}{40}$+$\frac{x+2}{40}$×8=1 | ||
| C． | $\frac{12x}{40}+\frac{x+2}{40}$×12=1 | D． | $\frac{12x}{40}+\frac{x+2}{40}$×8=1 |
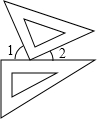一副三角板按如图方式摆放，且∠1的度数比∠2的度数大50°，设∠1=x°，∠2=y°，先根据题意列出二元一次方程组，再求解．