题目内容
如果x+y=m,x-y=n,那么2x+y= .
考点:解二元一次方程组
专题:
分析:把题干中给出2方程式相加即可求的x的值,相减即可求得y的值,即可解题.
解答:解:∵x+y=m,x-y=n,
∴(x+y)+(x-y)=m+n,x=
,
∵x+y=m,x-y=n,
∴(x+y)-(x-y)=m-n,y=
,
∴2x+y=m+n+
=
,
故答案为
.
∴(x+y)+(x-y)=m+n,x=
| m+n |
| 2 |
∵x+y=m,x-y=n,
∴(x+y)-(x-y)=m-n,y=
| m-n |
| 2 |
∴2x+y=m+n+
| m-n |
| 2 |
| 3m+n |
| 2 |
故答案为
| 3m+n |
| 2 |
点评:本题考查了加减消元法解二元一次方程组的方法,熟练运用加减消元法是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
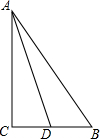 如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=64,且BD:CD=9:7,则点D到AB边的距离为
如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=64,且BD:CD=9:7,则点D到AB边的距离为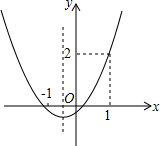 已知抛物线y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②a+b+c=2;③2a-b>0;④b>1.其中正确的结论个数是( )
已知抛物线y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②a+b+c=2;③2a-b>0;④b>1.其中正确的结论个数是( )