题目内容
 如图,已知△ABC.
如图,已知△ABC.(1)用直尺和圆规作△ABC的外接圆;
(2)若AB=8,AC=5,BC=7,求△ABC的外接圆半径R.
考点:作图—复杂作图,三角形的外接圆与外心
专题:
分析:(1)分别作AB、AC两边的垂直平分线,相交于点O,再以O为圆心,以OA长为半径画圆,⊙O即为所求的三角形的外接圆;
(2)利用余弦定理求得∠A的度数,然后过外接圆的圆心作BC的垂线,利用圆周角定理和三角函数即可求解.
(2)利用余弦定理求得∠A的度数,然后过外接圆的圆心作BC的垂线,利用圆周角定理和三角函数即可求解.
解答:解:(1)

圆O就是所求的圆;
(2)∵BC2=AB2+AC2-2AB•AC•cosA,
∴72=82+52-80cosA,
解得:cosA=
,
∴∠A=60°.
连接OB、OC,
则∠BOC=2∠A=120°,
∵OD⊥BC,
∴∠BOD=
∠BOC=60°,BD=
BC=3.5.
∴OB=
=
=
.

圆O就是所求的圆;
(2)∵BC2=AB2+AC2-2AB•AC•cosA,
∴72=82+52-80cosA,
解得:cosA=
| 1 |
| 2 |
∴∠A=60°.
连接OB、OC,
则∠BOC=2∠A=120°,
∵OD⊥BC,
∴∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴OB=
| ||
| sin∠BOD |
| ||||
|
7
| ||
| 3 |
点评:本题考查了作图-复杂作图,三角形的外接圆,圆周角定理,以及余弦定理,正确利用余弦定理求得∠A的度数是关键.

练习册系列答案
相关题目
御河中学校团委会要组织一次初三学生篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排78场比赛,则参赛球队的个数是( )
| A、11个 | B、12个 |
| C、13个 | D、14个 |
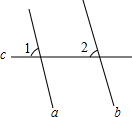 如图,a∥b,a、b被c所截,得到∠1=∠2的依据是( )
如图,a∥b,a、b被c所截,得到∠1=∠2的依据是( )| A、两直线平行,同位角相等 |
| B、两直线平行,内错角相等 |
| C、同位角相等,两直线平行 |
| D、内错角相等,两直线平行 |
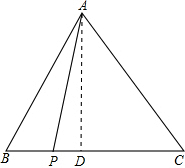 如图,在△ABC中,AB=AC=1,BC边上有2011个不同的点P1,P2,…,P2011,记mi=APi2+BPi•PiC(i=1,2,…,2011),则m1+m2+…+m2011=
如图,在△ABC中,AB=AC=1,BC边上有2011个不同的点P1,P2,…,P2011,记mi=APi2+BPi•PiC(i=1,2,…,2011),则m1+m2+…+m2011=