题目内容
14.若$\frac{m}{x+3}$-$\frac{n}{x-3}$=$\frac{8x}{{x}^{2}-9}$(x≠±3),则m、n的值是( )| A. | m=4,n=-4 | B. | m=-4,n=4 | C. | m=2,n=2 | D. | m=1,n=-4 |
分析 已知等式左边通分并利用同分母分式的减法法则计算,利用分式相等的条件求出m与n的值即可.
解答 解:已知等式整理得:$\frac{m(x-3)-n(x+3)}{{x}^{2}-9}$=$\frac{8x}{{x}^{2}-9}$,
可得(m-n)x-3m-3n=8x,
即m-n=8,-3m-3n=0,
解得:m=4,n=-4,
故选A
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
2.若计算(x-2m)(x+4)的结果不含x的一次项,则m的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | 2 |
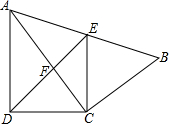 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB中点.